Nr.

1

2

3

4

5

6

1.	Eine Parabel mit der Funktion f1(x) wird von einer Geraden mit der Funktion f2(x) in den Punkten P1 und P2 geschnitten, wobei P2 der tieferliegende Punkt sein soll. Rechtwinklig zu der Geraden mit der Funktion f2(x) verläuft eine zweite Gerade mit der Funktion f3(x) durch den Punkt P2. Berechnen Sie:
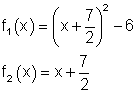
	a)	Die Schnittpunkte P1 und P2 von Parabel und Gerade.
	b)	Die Funktion f3(x) der rechtwinklig zu f2(x) verlaufenden Geraden.
	c)	Zeichnen Sie die Graphen der Funktionen.

	Ergebnisse
	a)	Schnittpunkte P1 und P2 von Parabel und Gerade.
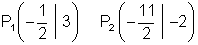
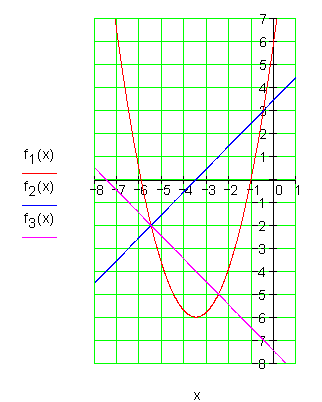
	b)	Die Funktion f3(x) der rechtwinklig zu f2(x) verlaufenden Geraden:
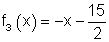
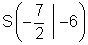
	c)	Scheitelpunktkoordinaten der Parabel: Graphen nebenstehend.

2.	Verschieben Sie die Parabel f(x) so in y- Richtung, dass sie die Gerade g berührt. Berechnen Sie die Verschiebung von f(x) und den Berührungspunkt.

	Ausführliche Lösung
	Die Parabel wird um 3,5 Einheiten nach unten verschoben.

3.	Eine Parabel mit der Funktion f1(x) wird von einer Geraden mit der Funktion f2(x) in den Punkten P1 und P2 geschnitten, wobei P2 der tieferliegende Punkt sein soll. Rechtwinklig zu der Geraden mit der Funktion f2(x) verläuft eine zweite Gerade mit der Funktion f3(x) durch den Punkt P2. Berechnen Sie:
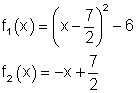
	a)	Die Schnittpunkte P1 und P2 von Parabel und Gerade.
	b)	Die Funktion f3(x) der rechtwinklig zu f2(x) verlaufenden Geraden.
	c)	Zeichnen Sie die Graphen der Funktionen.

	Ergebnisse
	a)	Schnittpunkte P1 und P2 von Parabel und Gerade.
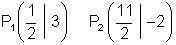
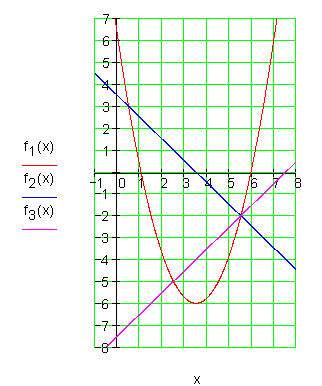
	b)	Die Funktion f3(x) der rechtwinklig zu f2(x) verlaufenden Geraden:
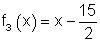
	c)	Scheitelpunktkoordinaten der Parabel:

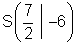
4.
	a)	Die Ursprungsgerade g(x) verläuft durch A( 1 | 6 ). Berechnen Sie die Schnittpunkte von f(x) mit g(x).
	b)	Welche Parallele zu g(x) berührt f(x)? Berechnen Sie den Berührungspunkt. Welche Parallelen zu g(x) haben mit f(x) keinen Berührungspunkt?

	Ausführliche Lösungen
	a)
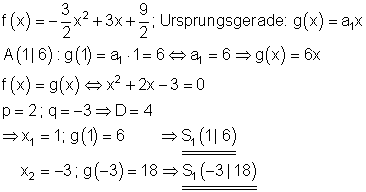
	b)

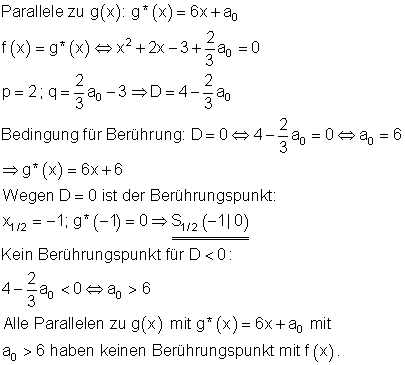
5.	Eine Parabel schneidet die Ordinatenachse (y- Achse) im Punkt P1 und wird in den Punkten P2 und P3 von einer Geraden mit der Funktion f1(x) geschnitten. Berechnen Sie:
	a)	Die Punkte P2 und P3.
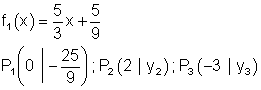
	b)	Die Funktion der f2(x) der Parabel.
	c)	Die Scheitelpunktform von f2(x).
	d)	Den Scheitelpunkt.
	e)	Die Achsenschnittpunkte.

	Ergebnisse
	a)	Die Punkte P2 und P3:
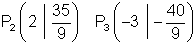
	b)	Die Funktion f2(x) der Parabel:
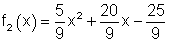
	c)	Die Scheitelpunktform von f2(x):
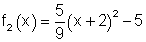
	d)	Den Scheitelpunkt:
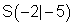
	e)	Die Achsenschnittpunkte:

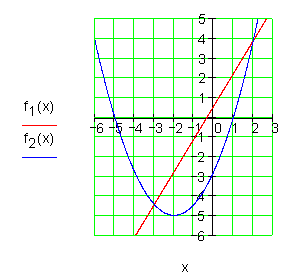
6.

Gegeben sind eine Parabel und eine Gerade durch ihre Wertetabelle. Wie liegen Parabel und Gerade zueinander? Auf welchem Bereich verläuft die Parabel oberhalb der Geraden?

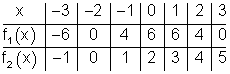
	Ergebnis
	Aus der Wertetabelle lässt sich ablesen: f1(x) ist die Funktionsgleichung der Parabel. f2(x) ist die Funktionsgleichung der Geraden. Parabel und Gerade schneiden sich in S1 ( -2 | 9 ) und S2 ( 2 | 4 ). Die Parabel ist nach unten geöffnet. Die Parabel verläuft oberhalb der Geraden im Intervall I = { x | -2 < x < 4 }R