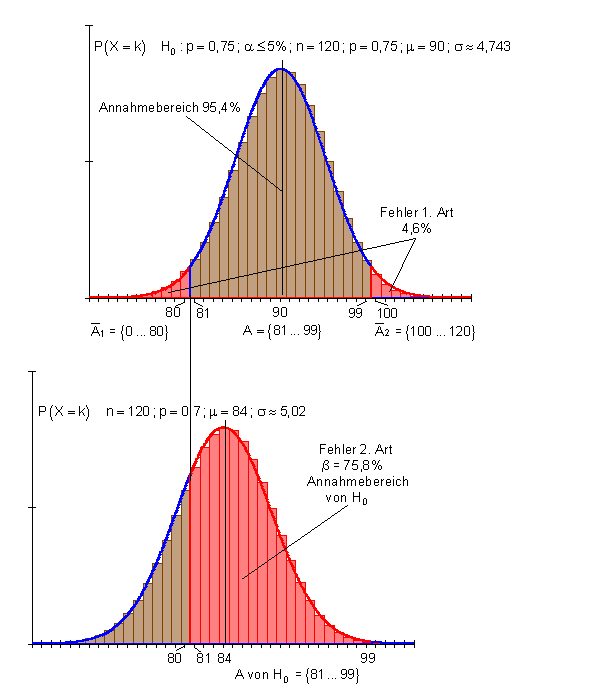
Es soll überprüft werden, ob der Anteil der Grundschüler, der zur Realschule wechselt, wie im vergangenen Jahr 75% beträgt. Da weder eine eindeutige Abweichung nach oben oder nach unten vermutet wird, handelt es sich um einen zweiseitigen Hypothesentest.
Die Hypothesen lauten:
Nullhypothese: H0: p = 0,75; Alternativhypothese H1: p ≠ 0,75.
Der Ablehnungsbereich, bestimmt durch das Signifikanzniveau von 5%, verteilt sich gleichmäßig auf beide Seiten.

Der Annahmebereich von H0 beinhaltet 81 bis 99 Entscheidungen für die Realschule.
Der Ablehnungsbereich von H0 beinhaltet 0 bis 80, bzw. 100 bis 120 Entscheidungen für die Realschule.
Falls p = 0,75 richtig ist, aber das Stichprobenergebnis zufällig in den Ablehnungsbereich fällt, lehnt man fälschlicherweise H0 ab. Die Wahrscheinlichkeit für den Fehler 1. Art ist gleich der Wahrscheinlichkeit für den Ablehnungsbereich.
1 - 0,954 = 0,046 (4,6%).
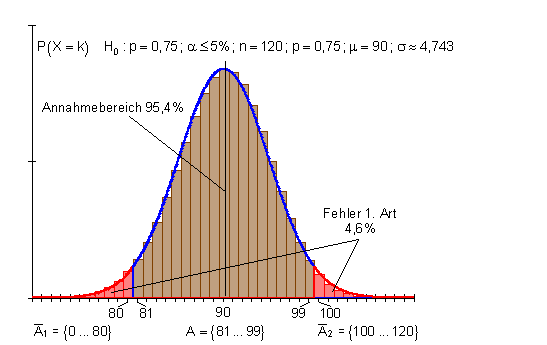
Falls H0 nicht gilt, sondern p = 0,7 richtig ist, d.h. die Hypothese p = 0,75 ist falsch, aber das Stichprobenergebnis fällt zufällig im Annahmebereich von H0 , nimmt man H0 fälschlicherweise an. Die Wahrscheinlichkeit dafür, diesen Fehler zu machen ist der Fehler 2. Art.
Man berechnet diesen Fehler, indem man unter der Annahme, dass p = 0,7 richtig ist, die Wahrscheinlichkeit des Annahmebereichs von H0 bestimmt.
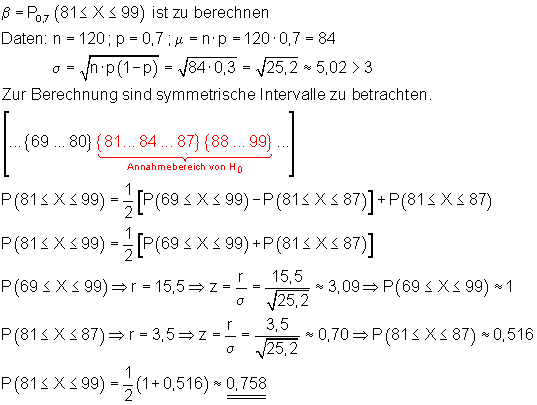
Falls H0 falsch und p = 0,7 richtig ist, fällt das Ergebnis dennoch zu 75,8% in den Annahmebereich von H0.
Die Nullhypothese würde fälschlicherweise angenommen werden. Dieser Fehler heißt Fehler 2. Art. Er beträgt 75,8% und ist im Vergleich zum Fehler 1. Art mit 4,6% sehr groß.