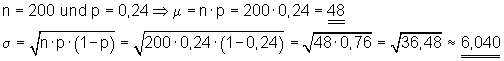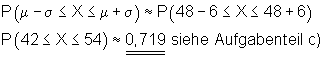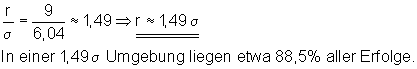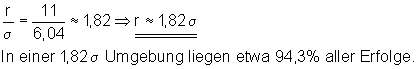195	Ausführliche Lösungen:
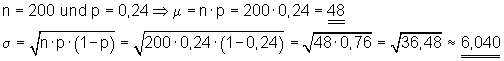
	a)	Die Anzahl der Erfolge beträgt genau 48
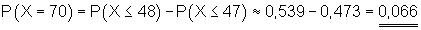
	b)	Die Anzahl der Erfolge beträgt höchstens 65
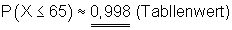
	c)	Die Anzahl der Erfolge liegt zwischen 42 und 54 (einschließlich)
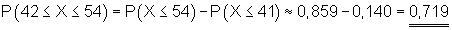
	d)	Die Anzahl der Erfolge liegt zwischen 36 und 60 (einschließlich)
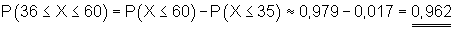
	e)	Die Anzahl der Erfolge liegt zwischen 30 und 66 (einschließlich)
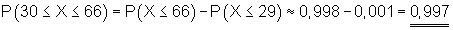
	f)	Die Anzahl der Erfolge liegt in der einfachen Sigma- Umgebung
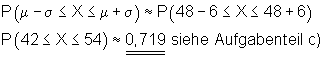
	g)	Die Anzahl der Erfolge liegt in der doppelten Sigma- Umgebung
	h)	Die Anzahl der Erfolge liegt in der dreifachen Sigma- Umgebung
	i)	In welcher Sigma- Umgebung liegen 90% aller Erfolge? Ansatz mit r = 10. Der gesuchte Radius liegt zwischen den Werten 9 und 10. Da es sich bei der Binomialverteilung um eine diskrete Verteilung handelt, muss man sich für den Radius entscheiden, der der gewünschten Wahrscheinlichkeit am nächsten liegt. In diesem Fall ist das der Radius r = 9. Teilt man diesen Wert durch Sigma, dann lässt sich der Radius als vielfaches von Sigma darstellen.
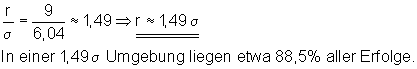
	j)	In welcher Sigma- Umgebung liegen 95% aller Erfolge? Ansatz mit r = 12. Der gesuchte Radius liegt zwischen den Werten 11 und 12. Der Radius r = 11 liegt der gewünschten Wahrscheinlichkeit am nächsten.
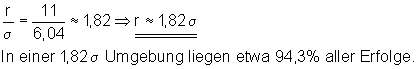
	k)	In welcher Sigma- Umgebung liegen 99% aller Erfolge? Ansatz mit r = 14. Der gesuchte Radius hat den Wert r = 15
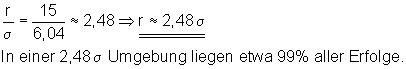