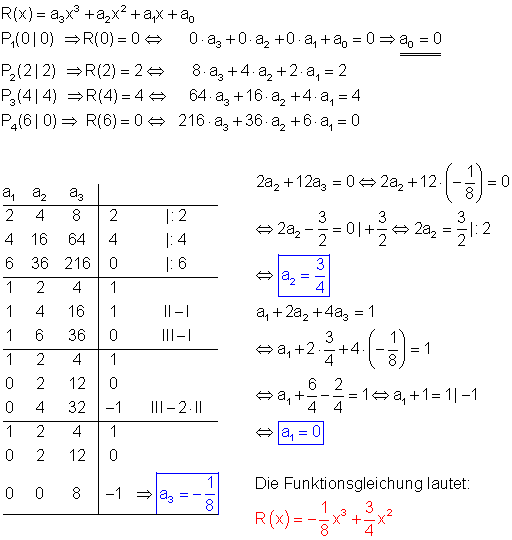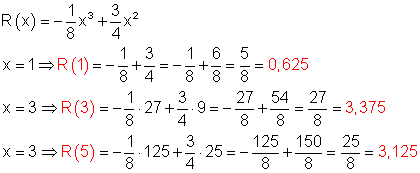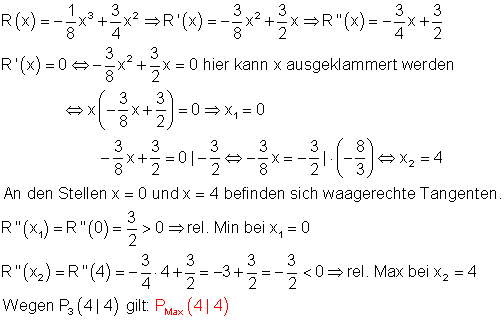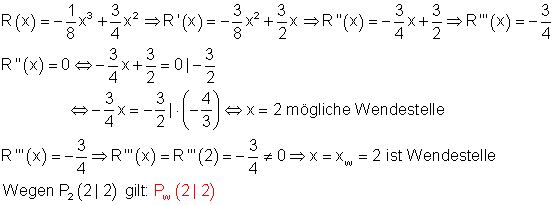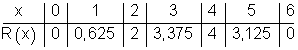084	Ausführliche Lösungen:
	a)	Bestimmen Sie die Funktion R(x) in Abhängigkeit von der Dosis x.
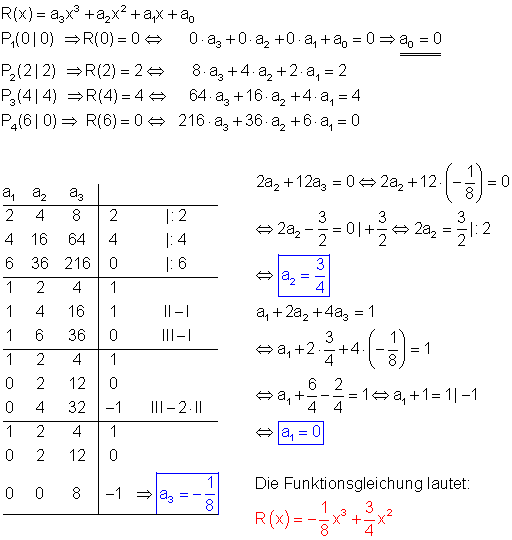
	b)	Funktionswerte für x = 1 ; 3 ; und 5
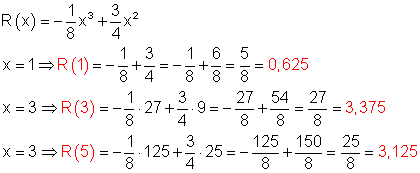
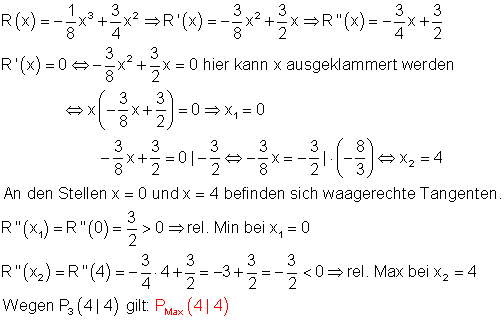
	c)	Für welchen Dosiswert ist die Reaktion am stärksten? Gesucht ist die maximale Reaktionsstärke in Abhängigkeit von der Dosis. Die maximale Reaktionsstärke entspricht dem Maximum von R(x). Für einen Dosiswert von x = 4 ist die Reaktion am stärksten.
	d)	Bei welcher Dosis reagiert die Pflanze am empfindlichsten auf das Düngemittel? Die momentane Änderungsrate von R(x) ist ein Maß für die Empfindlichkeit der Pflanze auf das Düngemittel. Da die momentane Änderungsrate einer Funktion deren Steigung entspricht, wird der Dosiswert x gesucht, bei der die Steigung des Graphen von R(x) maximal ist. Der Wendepunkt kennzeichnet den Punktmit maximaler, bzw. minimaler Steigung. 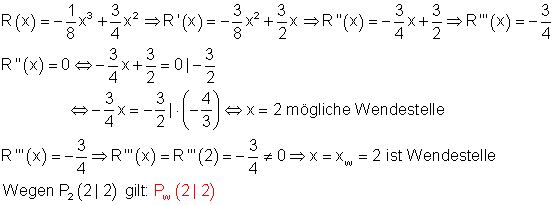Bei einen Dosiswert von x = 2 reagiert die Pflanze am empfindlichsten auf das Düngemittel.
	e)	Bestimmen Sie die Achsenschnittpunkte.
	f)	Tragen Sie alle bisher bekannten Werte in eine Wertetabelle ein.
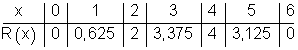
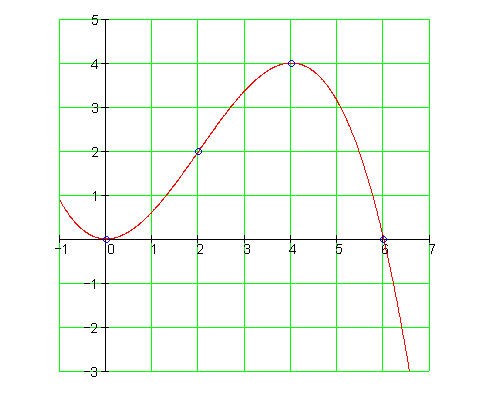
	g)	Zeichnen Sie den Graphen in ein geeignetes Koordinatensystem.
	h)	P1 ( 0 | 0 ) Wird kein Düngemittel gegeben, ist auch keine Reaktion der Pflanze zu erwarten. PMax ( 4 | 4 ) Bei der Dosis x = 4 ist die Reaktion der Pflanze am stärksten (Düngungsoptimum). Wird mehr gegeben, so spricht man von Überdüngung mit geringerem Erfolg. Pw ( 2 | 2 ) Die Empfindlichkeit der Pflanze auf Dünger ist bei der Dosis x = 2 am stärksten. Dort bewirken geringste Dosisverstärkungen die stärkste Reaktionszunahme. P4 ( 6 | 0 ) Bei der Dosis x = 6 erfolgt keine Reaktion der Planze mehr. Für x > 6 ist das Ergebnis schlechter als ohne Düngung. Die Pflanze würde sich zurückentwickeln, bzw. absterben. Aus Kostengründen würde der Landwirt sich möglicherweise für eine Dosierung im Bereich 2 < x < 4 entscheiden.