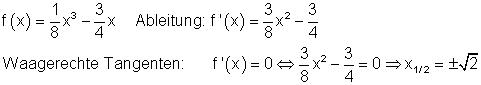
Die Ableitung f'(x) hat bei x1/2 einfache Nullstellen und wechselt das Vorzeichen.
Also hat f(x) zwei Extrempunkte.
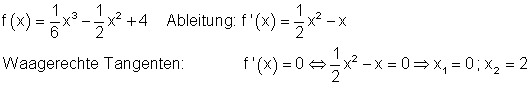
Die Ableitung f'(x) hat bei x1/2 einfache Nullstellen und wechselt das Vorzeichen.
Also hat f(x) zwei Extrempunkte.
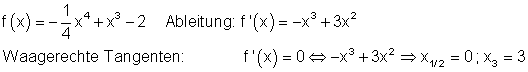
Die Ableitung f'(x) hat an der Stelle x1/2 = 0 eine doppelte Nullstelle, das bedeutet, es findet kein Vorzeichenwechsel statt. Also hat f(x) an dieser Stelle keinen Extrempunkt. x3 = 3 ist einfache Nullstelle von f'(x), dort findet ein Vorzeichenwechsel statt.
Also hat f(x) an dieser Stelle einen Extrempunkt.