209	Ausführliche Lösung:
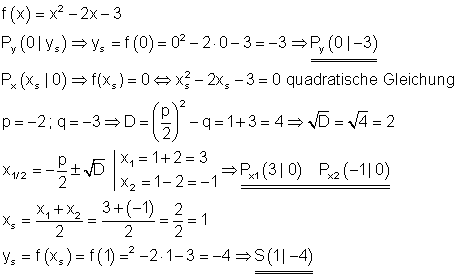
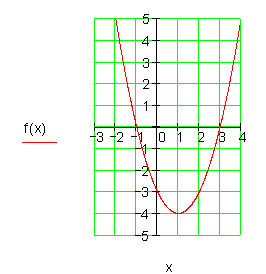
	Vorgehensweise: Die x- Koordinate des Scheitelpunktes liegt symmetrisch zu den Nullstellen. Der Schnittpunkt mit der y- Achse hat die x- Koordinate 0, also f(0) = ys. Schnittpunkte mit der x- Achse haben die y- Koordinate 0, also f(xs) = 0. Das führt auf eine quadratische Gleichung, deren Lösung die x- Koordinaten derAchsenschnittpunkte sind.
	Der Graph einer quadratischen Funktion ist eine Parabel. Jede Parabel ist symmetrisch zu der Achse, die durch den Scheitelpunkt führt. Falls es Schnittpunkte mit der x- Achse gibt, liegen auch diese symmetrisch zu der Scheitelachse. Die x- Koordinate des Scheitelpunktesliegt genau in der Mitte zwischen den Nullstellen.