In diesem Beitrag stelle ich die Grundlagen des Hypothesentests vor. Als Erstes definiere ich die Nullhypothese und die alternative Hypothese. Danach stelle ich die Reihenfolge beim Testen von Hypothesen vor. Anschließend zähle ich die Regeln zum Aufstellen der Hypothese auf. Als Nächstes zeige ich die beiden Möglichkeiten der Nullhypothese und die alternative Hypothese anhand mehrerer Beispiele. Es können übrigens Fehler beim Testen von Hypothesen auftreten. Deshalb stelle ich Entscheidungsregeln und deren Fehlermöglichkeiten vor. Zum Schluss beantworte ich die Frage, wann was wie zu testen ist.
Definitionen
Wer Entscheidungen zu treffen hat, weiß oft erst im Nachhinein ob seine Entscheidung richtig war. Die Unsicherheit eine Entscheidung zu treffen, beinhaltet immer eine gewisse Fehlerwahrscheinlichkeit. Der Hypothesentest gibt uns eine Richtlinie für die Wahl einer Alternativentscheidung. Wir treffen unsere Entscheidung auf der Grundlage dessen, was wir für richtig erachten. Das nennen wir die Nullhypothese.
Eine Alternativentscheidung nennen wir alternative Hypothese.
Reihenfolge beim Hypothesentest:
- Formulierung der Nullhypothese H0 und der Alternativhypothese H1.
- Festlegung des Signifikanzniveaus.
- Bestimmung des Annahme- und Ablehnungsbereichs der Nullhypothese.
- Ziehung der Stichprobe.
- Treffen der Testentscheidung und Interpretation:
Liegt das Ergebnis der Stichprobe innerhalb des Annahmebereichs, wird H0 angenommen, anderenfalls abgelehnt.
Regeln zum Aufstellen der Hypothese
- Was ich zeigen oder beweisen will, gehört in die Alternativhypothese
- Das Gleichheitszeichen gehört immer in die Nullhypothese
- Beim aufstellen der Nullhypothese geht man davon aus, „Alles bleibt beim alten, nichts hat sich geändert“
Die Annahme der Nullhypothese führt immer zur Ablehnung der Alternativhypothese, ist aber kein Beweis dafür, dass die Nullhypothese stimmt. Die Ablehnung der Nullhypothese führt zur Annahme der Alternativhypothese.
Beispiel 1 zum Hypothesentest
Die Befragung aller Studenten einer Fachhochschule ergab im letzten Jahr, dass 10% der befragten Studenten mit dem Mensaessen unzufrieden waren. Es wird vermutet, dass die Unzufriedenheit im laufenden Semester sogar noch zugenommen hat. Das Mensa-Organisationsteam steht nun vor der Entscheidung, ob Maßnahmen zur Verbesserung der Qualität des Essens ergriffen werden müssen. Um eine Entscheidung treffen zu können, werden in einer Umfrage 100 Studenten befragt.
Möglichkeit a)
Sind mehr als 10 Studenten mit dem Essen unzufrieden, so soll die Qualität des Essens verbessert werden. In der ersten Umfrage erklärten 12 Studenten, mit dem Mensaessen unzufrieden zu sein.
Möglichkeit b)
Das Mensateam ist sich der Zufälligkeit von Stichprobenergebnissen bewusst und lässt in einer 2. Umfrage wieder 100 Studenten befragen. Dabei gibt sich das Team mit einer Sicherheit von 95% mit dem Befragungsergebnis zufrieden. Es erklären 13 Studenten, mit dem Essen nicht zufrieden zu sein.
Wie wird das Team in beiden Fällen entscheiden?
Die Entscheidung soll über einen Hypothesentest gefunden werden.
Zu zeigen ist p > 0,1
Das heißt: Mehr als 10% aller Studenten sind mit dem Essen unzufrieden.
Damit liegen die Null- und die Alternativhypothese fest.
H0: p ≤ 0,1 und H1 > 0,1.
a) Es wird die H0-Hypothese getestet.
Sie wird angenommen, bzw. beibehalten, wenn die Zahl der Studenten im Annahmebereich und sie wird abgelehnt, wenn die Zahl der Studenten im Ablehnungsgsbereich liegt.
H0: p ≤ 0,1
Der Annahmebereich A ist also: {0; 1; …; 10} .
Der Ablehnungsbereich \overline {A} ist folglich : {11; 12; …. 100}
Beim 1. Test erklärten 12 Studenten, mit dem Essen unzufrieden zu sein.
Die H0-Hypothese würde damit abgelehnt, aber dies könnte wegen der Zufälligkeit der Stichprobe falsch sein, wenn der tatsächliche Anteil der unzufriedenen in der Grundgesamtheit (Menge aller Studenten der Fachhochschule) tatsächlich 10% ist. Man begeht also bei der Ablehnung der H0-Hypothese mit einer gewissen Wahrscheinlichkeit einen Fehler.
Dieser Fehler, auch als Irrtumswahrscheinlichkeit des Hypothesentests bezeichnet, berechnet sich aus der Ablehnungswahrscheinlichkeit.
P(X ≥ 11) = 1 – P(X ≤ 10) ≈ 1 – 0,583 = 0,417 (siehe Tabelle 1).
Berechnung mit dem GTR Casio fx-CG20:
Eine Einführung in den Casio fx-CG20 und Casio fx-CG50 findest du hier.
Dort findest du auch eine Anleitung, wie man den Casio fx-CG20 auf den Casio fx-CG50 updaten kann.
Eingabebeispiel mit ähnlichen Zahlen für P(X ≥ k) (alle Beispiele zum grafikfähigen Taschenrechner hier).
P(X ≥ 11) = 1 – BinomialCD(10, 100, 0.1) = 0,4168…
Das heißt, mindestens 11 Studenten sind mit dem Essen unzufrieden.
Man muss also sagen:
„Unter der Annahme, dass tatsächlich 10% aller Studenten unzufrieden sind, kommt es bei der angegebenen Befragung mit einer Wahrscheinlichkeit von ca. 41,7% zu einem solchen Ergebnis und damit zu fälschlichen Ablehnung der Nullhypothese“.
Eine Verteilungsfunktion soll das verdeutlichen:
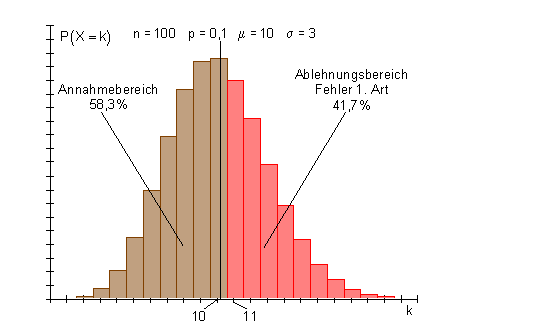
b) Beim 2. Hypothesentest wird ein Fehler von 5% zugestanden (Sicherheit von 95%).
Dadurch ändern sich Annahme- und Ablehnungsbereich.

Berechnung mit dem GTR Casio fx-CG20
Eingabebeispiel mit ähnlichen Zahlen für P(X ≥ k) ≤ α ⇒ k = ? und P(X ≥ k)
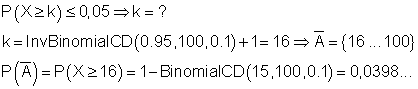
Während der Annahmebereich größer wird, wird der Ablehnungsbereich kleiner. Da das 2. Testergebnis mit 13 unzufriedenen Studenten in den neuen Annahmebereich fällt, wird die Nullhypothese angenommen. Das Mensateam sieht keine Veranlassung, das Essen zu verbessern. Erst wenn mehr als 15 Studenten mit dem Essen nicht zufrieden wären, würde die Nullhypothese abgelehnt, die Alternativhypothese angenommen und das Essen verbessert werden.
Eine Verteilungsfunktion soll das verdeutlichen:
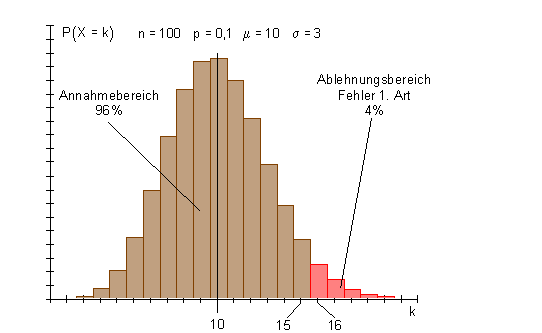
Die Wahrscheinlichkeit beim Testen einen gewissen Fehler zuzulassen, heißt Irrtumswahrscheinlichkeit. Sie wird in der Regel vor Durchführung des Zufallsexperimentes festgelegt. Dabei sind 1% und 5% übliche Werte. Sie ist die größte Wahrscheinlichkeit für eine irrtümliche Ablehnung der H0-Hypothese. Statt Irrtumswahrscheinlichkeit sagt man auch Signifikanzniveau.
Tabelle 1 zum Hypothesentest
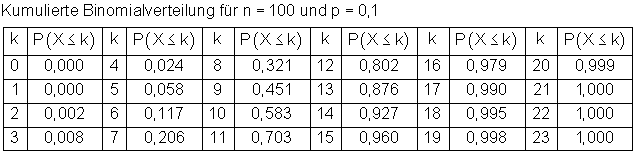
Ein Test, bei dem der Ablehnungsbereich oberhalb, also rechts vom Erwartungswert liegt, heißt Rechtsseitiger Hypothesentest. Vielfach wird dieses Verfahren dann benutzt , wenn die Alternativhypothese H1:p > a lautet, und H0: p ≤ a zu testen ist. Da die Binomialverteilung eine diskrete Verteilung darstellt, gelingt es oft nicht, den Ablehnungsbereich so zu bestimmen, dass die Irrtumswahrscheinlichkeit genau dem vorgegebenen Wert entspricht. Sie sollte aber nicht oberhalb des geforderten Wertes liegen.
Rechtsseitiger Hypothesentest
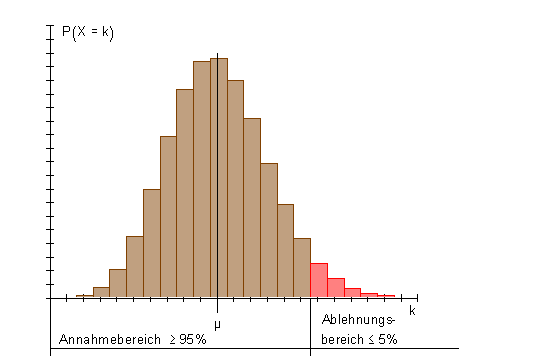
Ein Test, bei dem der Ablehnungsbereich unterhalb, also links vom Erwartungswert liegt, heißt Linksseitiger Hypothesentest. Vielfach wird dieses Verfahren dann benutzt , wenn die Alternativhypothese H1:p < a lautet, und H0: p ≥ a zu testen ist.
Linksseitiger Hypothesentest
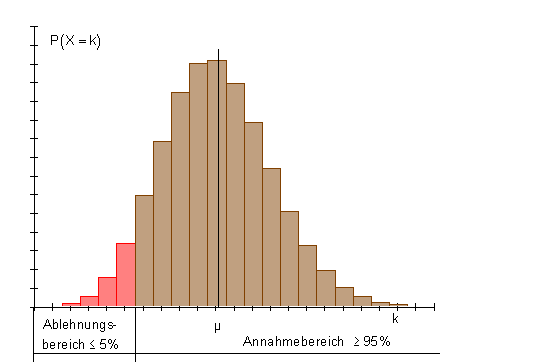
Fehler beim Hypothesentest
Die Entscheidung, die aufgrund eines Versuchsergebnisses (Test, Umfrage, …) getroffen wird kann falsch sein. Die zu testende Hypothese H0 ( höchstens 10% aller Studenten sind mit dem Essen unzufrieden) kann wahr oder falsch sein.
Man unterscheidet zwei Arten von Fehlern:
Fehler 1. Art: Die Nullhypothese wird verworfen, obwohl sie richtig ist.
Fehler 2. Art: Die Nullhypothese wird angenommen, obwohl sie falsch ist.
Der Fehler 2. Art lässt sich nur berechnen, wenn man für die Alternativhypothese eine andere Wahrscheinlichkeit, als für H0 annimmt.
Beispiel 2 (Alternativtest)
Ein Babybasar verkauft gebrauchte Kinderschuhe. Etwa 60% der Schuhe befinden sich in einem einwandfreien Zustand. Der Rest weist kleine Schäden auf. Ein neuer Lieferant behauptet, er könne gebrauchte Kinderschuhe liefern, von denen sich etwa 80% in einem einwandfreien Zustand befinden. Der Ladeninhaber möchte keine falsche Kaufentscheidung treffen und will die Behauptung des Lieferanten überprüfen.
Dazu testet er 20 Paar Kinderschuhe aus dem Sortiment des Anbieters.
Fall I:
Angenommen, die Behauptung des Lieferanten ist richtig, d.h. die Wahrscheinlichkeit für einwandfreie Schuhe ist p = 0,8.
Der Ladeninhaber bezweifelt die Aussage des Lieferanten, er geht von p < 0,8 aus.
Er stellt folgende Hypothesen auf:
Nullhypothese H0: p ≥ 0,8 und die Alternativhypothese H1: p < 0,8
Im Versuch mit n = 20 Paar Schuhen erwartet man μ = n · p = 20 · 0,8 = 16 einwandfreie Paare.
Wenn mindestens 16 Paar Schuhe einwandfrei sind, dann spricht das für die Behauptung des Liefereranten, dann soll H0 angenommen werden. Zufällig kann es auch zu weniger als 16 Paar einwandfreien Schuhen kommen, obwohl p = 0,8 ist. Die Nullhypothese soll abgelehnt werden, wenn weniger als 16 Paar Schuhe einwandfrei sind .
Mit welcher Wahrscheinlichkeit ist dies der Fall?
P(X ≤ 15) = 0,370 (siehe Tabelle 3),
Berechnung mit dem GTR Casio fx-CG20
Eingabebeispiel mit ähnlichen Zahlen für P(X ≤ k)
P(X ≤ 15) = BinomialCD(15, 20, 0.8) = 0,370…
Mit einer Wahrscheinlichkeit von 37% kann es vorkommen, dass bei dem Test weniger als 16 Paar Schuhe einwandfrei sind, obwohl 80% der Schuhe einwandfrei sind. Man würde also mit einer Wahrscheinlichkeit von 37% irrtümlicher Weise die Nullhypothese ablehnen.
Fall II:
Angenommen, die Schuhe des Lieferanten sind auch nur zu 60% einwandfrei.
Mit dieser Annahme stellt der Ladenbesitzer folgende Hypothesen auf:
Nullhypothese H0: p ≤ 0,6 und die Alternativhypothese H1: p > 0,6
Im Versuch mit n = 20 Paar Schuhen erwartet man μ = n · p = 20 · 0,6 = 12 einwandfreie Paare.
Wenn mehr als 12 einwandfreie Paar Schuhe gefunden werden, spricht das eher gegen die Vermutung des Ladenbesitzers ( p = 0,6 ).
Zufällig kann es aber auch zu mehr als 12 einwandfreien Paaren kommen, obwohl p = 0,6 ist.
Die Nullhypothese soll abgelehnt werden, wenn mehr als 12 Paar Schuhe einwandfrei sind .
Mit welcher Wahrscheinlichkeit ist dies der Fall?
P(X > 12) = P(X ≤ 20) – P(X ≤ 12) = 1 – 0,584 = 0,416 (siehe Tabelle 2).
Berechnung mit dem GTR Casio fx-CG20
Eingabebeispiel mit ähnlichen Zahlen für P(X ≥ k)
P(X > 12) = P(X ≥ 13) = 1 – BinomialCD(12, 20, 0.6) = 0,4158…
Mit einer Wahrscheinlichkeit von 41,6% kann es vorkommen, dass bei dem Test mehr als 12 Paar Schuhe einwandfrei sind, obwohl nur 60% der Schuhe einwandfrei sind. Man würde also mit einer Wahrscheinlichkeit von 41,6% irrtümlicher Weise die Nullhypothese ablehnen.
In beiden Fällen ist die Wahrscheinlichkeit dafür, eine Fehlentscheidung zu treffen ziemlich groß (Fall I 37%, Fall II 41,6%).
Bevor der Test durchgeführt wird, ist es sinnvoll sich dafür zu entscheiden, bei welcher Anzahl von einwandfreien Schuhen man p = 0,8 oder p = 0,6 für richtig halten will. Eine solche Entscheidung ist willkürlich. Dabei sollte man nicht zu nah am Erwartungswert liegen, damit die Wahrscheinlichkeit für eine Fehlentscheidung nicht zu groß wird.
Es wird folgende Entscheidungsregel aufgestellt:
Falls mindestens 15 Paar einwandfrei sind, wird p = 0,8 als richtig angesehen, sonst soll p = 0,6 gelten.
Die Hypothesen lauten: H0: p ≥ 0,8 und H1: p < 0,8.
Aus der Vorgabe folgen Annahme- und Ablehnungsbereich für H0.
Daher ist der Annahmebereich A = {15 … 20}.
Der Ablehnungsbereich ist folglich \overline{A} ={0 …14}.
Falls H0 abgelehnt werden muss, soll H1: p < 0,8 = 0,6 gelten.
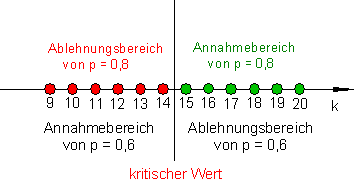
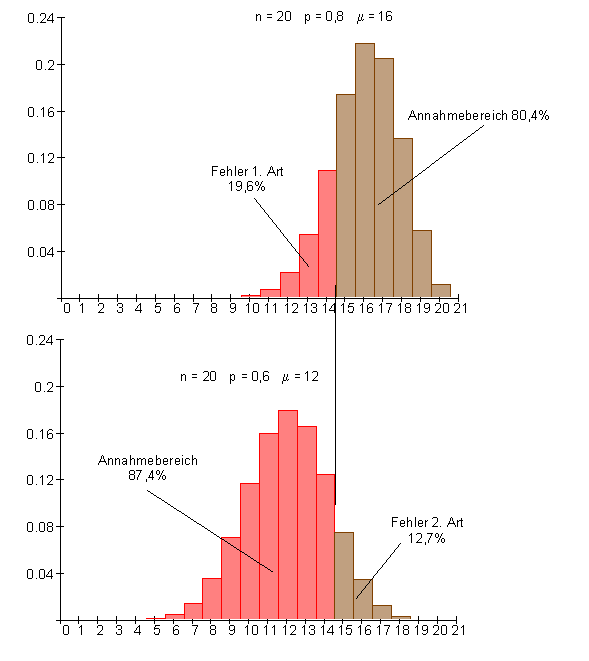
Fehlermöglichkeiten dieser Entscheidung:
1.p = 0,8 ist richtig, das bedeutet, der neue Lieferant kann wirklich Schuhe höherer Qualität liefern. Zufällig kann es vorkommen, das weniger als 15 Paar Schuhe einwandfrei sind. Dann würde man dem Lieferanten nicht glauben. Die Wahrscheinlichkeit einen solchen Fehler zu begehen beträgt
P80(X ≤ 14) = 0,296 (siehe Tabelle 3).
Berechnung mit dem GTR Casio fx-CG20:
Eingabebeispiel mit ähnlichen Zahlen für P(X ≤ k)
P80(X ≤ 14) = BinomialCD(14, 20, 0.8) = 0,1957…
Das bedeutet, wenn man einen solchen Zufallsversuch mit 20 Paar Schuhen sehr oft durchführen würde, könnte man in 19,6% der Fälle ein Ergebnis erwarten, das gegen die tatsächliche Qualität der Schuhe spricht.
Fehler 1. Art:
In 19,6% aller Fälle würde die wahre Hypothese, (die Schuhe des neuen Lieferanten sind besser) verworfen werden.
2. p = 0,6 ist richtig, das bedeutet, der neue Lieferant kann auch keine besseren Schuhe liefern, als die, die man bereits hat. Zufällig kann es aber vorkommen, dass trotzdem 15 oder mehr Paar Schuhe einwandfrei sind. Man würde in diesem Fall fälschlicherweise die Schuhe des neuen Lieferanten für besser halten. Die Wahrscheinlichkeit einen solchen Fehler zu begehen beträgt
P60(X ≥ 15) = P(X ≤ 20) – P(X ≤ 14) = 1 – 0,874 = 0,126 (siehe Tabelle 2).
Berechnung mit dem GTR Casio fx-CG20
Eingabebeispiel mit ähnlichen Zahlen für P(X ≥ k)
P60(X ≥ 15) = 1 – BinomialCD(14, 20, 0.6) = 0,1255…
Das bedeutet, wenn man einen solchen Zufallsversuch mit 20 Paar Schuhen sehr oft durchführen würde, könnte man in 12,6% der Fälle ein Ergebnis erwarten, dass die Qualität der Schuhe höher angesehen wird, als sie tatsächlich ist.
Fehler 2. Art:
In 12,6% aller Fälle würde die falsche Hypothese, (die Schuhe des neuen Lieferanten sind besser) nicht verworfen werden.
Zusammenfassung der Fehlerarten beim Hypothesentest:

![]()
Um den Fehler 2. Art zu berechnen, betrachtet man den Annahmebereich der Nullhypothese unter der Voraussetzung das die Alternativhypothese gilt. Der Fehler 2. Art ist die Wahrscheinlichkeit dafür, dass ein Testergebnis in den Annahmebereich der Nullhypothese fällt, obwohl die Alternativhypothese gilt.
Irrtumswahrscheinlichkeit wird vorgegeben
Wird eine Irrtumswahrscheinlichkeit vorgegeben, dann ergibt sich daraus der Annahme und der Ablehnungsbereich.

Berechnung mit dem GTR Casio fx-CG20
Eingabebeispiel mit ähnlichen Zahlen für P(X ≤ k) ≤ α ⇒ k = ? und P(X ≤ k) und P(X ≥ k) (siehe jeweils hier)
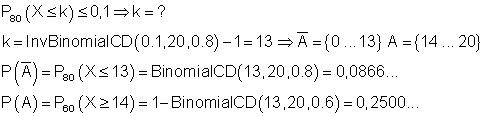
Dadurch, dass die Wahrscheinlichkeit für einen Fehler 1. Art auf mehr als die Hälfte verringert wurde, hat sich der Fehler 2. Art etwa verdoppelt.
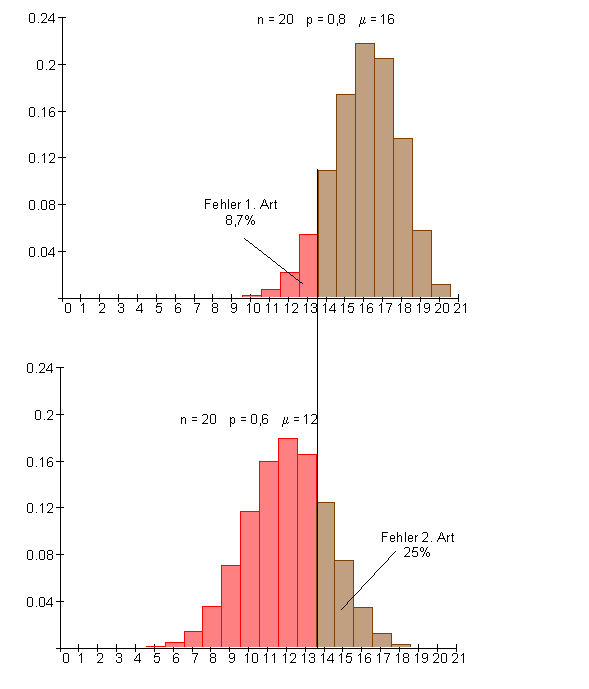
Falls die Hypothese p = 0,8 wahr ist, ist die Wahrscheinlichkeit dafür, dass sie aufgrund eines Testergebnisses fälschlicherweise abgelehnt wird 8,7%.
Denn in 8,7% aller Fälle liegt das Testergebnis im Ablehnungsbereich von p = 0,8.
Falls die Hypothese p = 0,6 wahr ist, ist die Wahrscheinlichkeit dafür, dass sie aufgrund eines Testergebnisses fälschlicherweise abgelehnt wird 25%.
Denn in 25% aller Fälle liegt das Testergebnis im Annahmebereich von p = 0,8.
Tabelle 2:

Tabelle 3:

Wann ist was wie zu testen beim Hypothesentest?
Aufstellen der Nullhypothese (H0) und der Gegenhypothese (H1).
Die Nullhypothese hängt von der jeweiligen Interessenlage ab.
![]()
In beiden Fällen wird für die Berechnung p = p0 verwendet.
Verschiedene Interessengruppen stellen also unterschiedliche Nullhypothesen auf. Das hat zur Folge, dass Annahme- und Ablehnungsbereich für die Interessengruppen unterschiedlich sind. Auch die Art des durchzuführenden Tests hängt von der jeweilig aufgestellten Nullhypothese ab.

Grundsätzlich kann man davon ausgehen, dass unterschiedliche Interessengruppen gegensätzliche (konträre) Nullhypothesen aufstellen.
Rechenhelfer für die Binomialverteilung
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Dazu findest du hier weitere Beispiele zum Hypothesentest.
Aufgaben zum Hypothesentest I.
Außerdem Hypothesentest II.

