In den bisherigen Beiträgen konnten wir mit übersichtlichen Ergebnisbäumen arbeitet. Doch diese Methode hat ihre Grenzen. Das zeigt schon allein das Beispiel des mehrmaligen Wurfes eines Würfels. Hier beschäftigen wir uns mit der Ereignissen, die in einer bestimmten Reihenfolge erfolgen. Mit anderen Worten in einer bestimmten Kombination. Deshalb spricht man hier auch von der Kombinatorik.
Dabei unterscheidet man geordnete und ungeordnete Stichproben. Außerdem mit und ohne Zurücklegen.
Wenn du auf einen Link klickst, gelangst du sofort zu dem entsprechenden Kapitel
- Geordnete Stichprobe mit Zurücklegen
- Geordnete Stichprobe ohne Zurücklegen
- Mathematische Fakultät
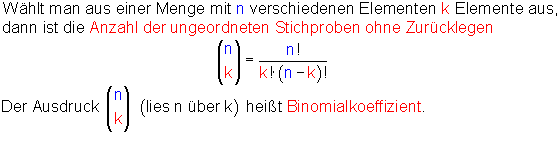
- Ungeordnete Stichprobe ohne Zurücklegen
- Zusammenfassung
- Lösungen der Übungen
Geordnete Stichprobe mit Zurücklegen
Beispiel Kombinationen mit Würfel:
Wir werfen einen Würfel k mal. Beziehungsweise wir ziehen k mal eine Kugel aus einer Urne mit Kugeln von 1 bis 6. Und zwar mit Zurücklegen.
Dann betrachten wir Ereignis A: Mit jedem Wurf beziehungsweise Zug erhält man eine 4.
a) Wie groß ist die Wahrscheinlichkeit bei jedem der k Würfe bzw. Züge eine 4 zu erhalten?
b) Wie viele Elemente enthält die Ergebnismenge, also die Anzahl aller Möglichkeiten?
Lösung:
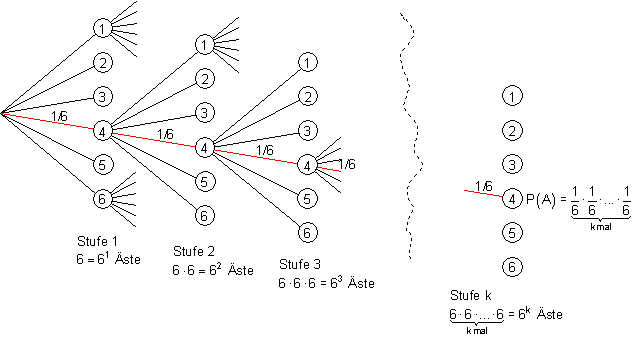
a) Für alle Ergebnisse können wir die gleiche Wahrscheinlichkeit annehmen. Mit anderen Worten, es handelt sich um ein Laplace-Experiment. Deshalb gilt für die Wahrscheinlichkeit, nach jeder Stufe eine 4 zu erhalten:
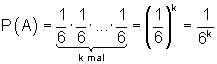
b) Da die Anzahl der Äste im Baumdiagramm sich mit jeder Stufe versechsfachen, gilt für die k-te Stufe:

Wenn man man diese Gesetzmäßigkeit verallgemeinert, erhält man die Rechenregel:
Wenn sich in einer Urne n gleichartige Kugeln mit den Nummern 1, 2, …, n befinden, wobei k mal mit zurücklegen gezogen wird, dann ist die Anzahl der Kombinationen nk.
Formel: Kombinationen geordnete Stichprobe mit Zurücklegen

Beispiel Kombinationen Fußballwette:
Bei der Fußballwette (Toto) muss man für 11 Spiele an einem Wochenende das Ergebnis vorhersagen. Wenn man meint, dass die Heimmannschaft gewinnt, eine 1. Für die Gastmannschaft dagegen eine 2. Für ein Unentschieden schließlich eine 0.
a) Wie viele Möglichkeiten gibt es, einen Toto-Tippzettel auszufüllen?
b) Wie groß ist die Wahrscheinlichkeit für einen Tipp mit 11 richtigen?
Lösung:
a) Zuerst erstellen wir ein Urnenmodell:
Eine Urne enthält drei Kugeln mit den Nummern 0; 1 und 2. Dann ziehen wir 11 mal mit Zurücklegen.

b)

Übung Kombinationen Zahlenschloss:
Ein Zahlenschloss fürs Fahrrad besteht aus vier unabhängig voneinander beweglichen Rädern. Diese enthalten jeweils 6 Ziffern von 1 bis 6. Das Schloss öffnet sich nur bei einer bestimmten Zahlenkombination. Wie viele Kombinationen hat das Fahrradschloss? Und wie groß ist die Wahrscheinlichkeit, bei der ersten Einstellung das Schloss zu öffnen?
Die Lösung hierzu ist unten.
Übung Kombinationen Alphabet:
Wir ziehen aus den 26 Buchstaben des Alphabets nacheinander blind drei Buchstaben mit Zurücklegen. Wie groß ist die Wahrscheinlichkeit dreimal denselben Buchstaben zu ziehen?
Die Lösung dazu findest du unten.
Geordnete Stichprobe ohne Zurücklegen
Beispiel Kombinationen vierfarbige Kugeln:
In einer Urne liegen 4 Kugeln. Davon ist je eine rot, gelb, grün und blau. Dann ziehen wir eine Kugel, registrieren die Farbe, legen die Kugel zur Seite und wiederholt den Vorgang.
Insgesamt sind 4 Züge möglich, dann ist die Urne leer.
Wie viele Elemente enthält die Ergebnismenge? Mit anderen Worten: wie groß ist die Anzahl aller Möglichkeiten?
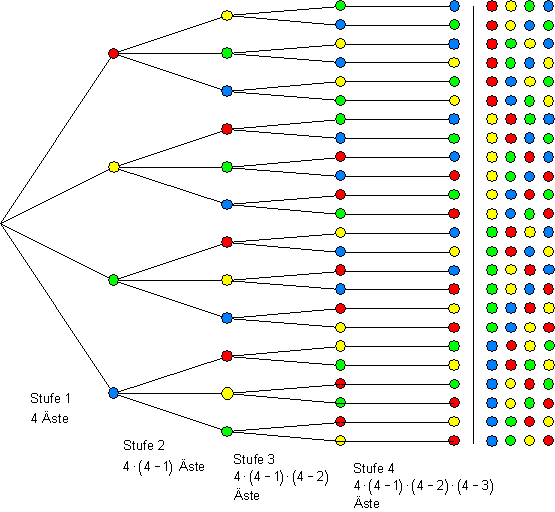
Wie wir anschließend aus dem Baumdiagramm ablesen, verringert sich von Stufe zu Stufe die Anzahl der Äste um 1.
![]()
Die aus dem Baumdiagramm abzulesende Gesetzmäßigkeit können wir verallgemeinern.
Betrachtet man nun eine Urne mit n Kugeln nummeriert von 1 bis n und führt k Züge ohne zurücklegen durch, so gilt für die Anzahl der Möglichkeiten:
![]()
Dazu gibt es einen mathematischen Begriff:
Mathematische Fakultät
Ein Produkt, bei dem jeder Folgefaktor um 1 erniedrigt wird, nennt man Fakultät.

Formel: Kombinationen geordnete Stichprobe ohne Zurücklegen:
Beispiel Kombinationen Passwort:
Z. B. ist ein Computerprogramm durch ein Passwort geschützt. Dieses Passwort besteht aus 4 unterschiedlichen Buchstaben.
a) Wie viele Passwörter sind möglich?
b) Mit welcher Wahrscheinlichkeit kann der Code mit einem Versuch geknackt werden?
Lösung:
a) Es stehen alle 26 Buchstaben des Alphabets genau einmal zur Verfügung. Für den ersten Buchstaben des Wortes kommen also alle 26 Buchstaben des Alphabets in Frage. Für den zweiten dann nur noch 25 usw.. Es handelt sich um eine geordnete Stichprobe ohne Zurücklegen. Aus n = 26 Buchstaben werden k = 4 Buchstaben gezogen. Deshalb berechnet man so:
![]()
b) Weil es nur einen richtigen Code gibt, berechnet man die Erfolgswahrscheinlichkeit unmittelbar:
![]()
Übung Kombinationen Lostrommel:
In einer Lostrommel befinden sich 6 Lose mit den Nummern 1 bis 6. Ein Spieler zieht nacheinander drei Lose. Wenn er in der Reihenfolge die Nummern 2, 4 und 6 zieht, hat er gewonnen. Berechne die Wahrscheinlichkeit dafür!
Die Lösung ist wieder unten.
Ungeordnete Stichprobe ohne Zurücklegen
Beispiel Kombinationen Lotto:
Bei der Ziehung der Lottozahlen werden 6 Zahlen aus insgesamt 49 Zahlen gezogen. Dabei handelt es sich um ein Ziehen ohne zurücklegen.
![]()
Weil es bei der Ziehung nicht auf die Reihenfolge der gezogenen Zahlen ankommt, verringert sich die Anzahl der Möglichkeiten. Denn man muss ja nicht berücksichtigen, wie oft sich die gezogenen Zahlen anordnen lassen.
Wenn man z. B. die Zahlen 3, 12, 17, 22, 36 und 41 zieht, kann man sie auch in der Form 17, 22, 41, 3, 36 und 12 anordnen. Denn das hat für den Gewinn keine Bedeutung. Damit wir die Anzahl der Möglichkeiten beim Lotto berechnen, müssen wir die Anzahl der möglichen Vertauschungen der 6 Zahlen herausfinden. Anders ausgedrückt, wir müssen herausfinden, auf wie viele Kombinationen es für diese 6 Zahlen gibt.
In einer Urne befinden sich n = 6 Kugeln mit den Nummern von 1 bis 6. Wenn man nun der Reihe nach ohne Zurücklegen k = 6 mal zieht bis die Urne leer ist, hat man alle Kombinationen gefunden.
![]()
Wenn man aus einer Urne mit n Elementen ohne Zurücklegen zieht bis die Urne leer ist, dann spricht man von einer geordneten Vollerhebung. Dann ist n = k. Für n verschiedene Elemente gibt es deshalb n! Vollerhebungen.
Mit anderen Worten: Eine Menge aus n unterschiedlichen Elementen lässt sich auf n! verschiedene Arten anordnen. Kommen wir zurück zu unserem Lotto-Beispiel.
Bisher haben wir ermittelt, wie viele Möglichkeiten es gibt, aus 49 Zahlen 6 zahlen zu ziehen. Weil es bei der Auswertung nicht auf die Reihenfolge der gezogenen Zahlen ankommt, muss die Anzahl der Möglichkeiten durch 6! geteilt werden.
Damit wird die Anzahl der Möglichkeiten im Lotto 6 Richtige zu haben:
![]()
Formel Kombinationen ungeordnete Stichprobe ohne Zurücklegen:
Beispiel Kombinationen Karten:
Aus einem Kartenspiel mit 32 Karten werden 4 Karten gezogen. Wie groß ist die Wahrscheinlichkeit dafür, dass dies 4 Buben sind?Ungeordnete Stichprobe ohne Zurücklegen.
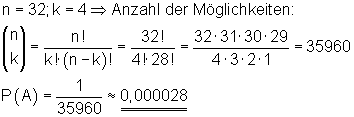
Übung Kartenspiel:
Wir ziehen aus einem Kartenspiel mit 32 Karten 8 Karten.
Wie groß ist die Wahrscheinlichkeit dafür, dass dies 8 Karo-Karten sind?
Die Lösung ist unten.
Berechnung mit einem Taschenrechner
Anspruchsvollere Taschenrechner haben für die oben genannten Formeln Funktionstasten.
Z. B. beim TI – 30 eco RS von Texas Instruments:
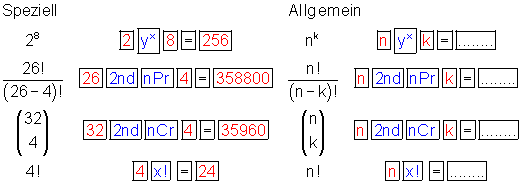
Zusammenfassung

Kombinatorik-Rechner
Interaktiv: Folgende Kombinationen kann man berechnen:
1. Anordnung von k Elementen.
2. Geordnete Stichprobe mit Zurücklegen.
3. Geordnete Stichprobe ohne Zurücklegen.
4. Ungeordnete Stichprobe ohne Zurücklegen.
5. Binominalverteilung.
Lösung der Übungen Fahrradschloss:
Ein Fahrradschloss (Zahlenschloss) besteht aus vier unabhängig voneinander beweglichen Rädern, die jeweils 6 Ziffern (von 1 bis 6) enthalten. Das Schloss öffnet sich nur bei einer ganz bestimmten Zahlenkombination.Wie viele Stellungen (Zahlenkombinationen) hat das Fahrradschloss und wie groß ist die Wahrscheinlichkeit, bei der ersten Einstellung das Schloss zu öffnen?
Lösung:
Wir modellieren mit einer Urne mit n = 6 Kugeln mit den Nummern 1 bis 6. Es wird k = 4 mal gezogen mit Zurücklegen.

Lösung der Übung Alphabet:
Wir ziehen aus den 26 Buchstaben des Alphabets nacheinander blind drei Buchstaben mit Zurücklegen. Wie groß ist dabei die Wahrscheinlichkeit dreimal denselben Buchstaben zu ziehen?
Lösung:
Wir nehmen eine Urne mit n = 26 Kugeln mit den Buchstaben A bis Z. Dann ziehen wir k = 3 mal mit Zurücklegen.

Lösung der Übung Lostrommel:
In einer Lostrommel befinden sich 6 Lose mit den Nummern 1 bis 6. Ein Spieler zieht nacheinander drei Lose. Wenn er in der Reihenfolge die Nummern 2, 4 und 6 zieht, hat er gewonnen. Berechne die Wahrscheinlichkeit dafür!
Lösung:
Zuerst berechnen wir die Anzahl der Möglichkeiten. Davon führt nur eine zum Gewinn: die Zahlenfolge 2, 4, 6. Es handelt sich also um eine geordnete Stichprobe ohne Zurücklegen. Aus n = 6 Zahlen werden k = 3 Zahlen gezogen.
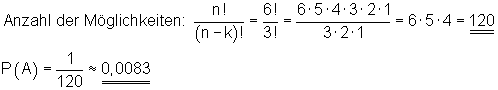
Lösung der Übung Kartenspiel:
Wir ziehen aus einem Kartenspiel mit 32 Karten 8 Karten.
Wie groß ist die Wahrscheinlichkeit 8 Karo-Karten zu ziehen?
Lösung:

Aufgaben hierzu. Darin die Berechnung der Wahrscheinlichkeiten beim Lotto spielen.
Außerdem Aufgaben zu Stichproben II. Darin Berechnung der Wahrscheinlichkeiten bei einem Multiple-Choice-Test.
Hier findest du Aufgaben zu Stichporben III.
Im nächsten Beitrag geht es um Zufallsvariable, Wahrscheinlichkeitsverteilungen, Erwartungswert.
Hier findest du eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung, darin auch Links zu Aufgaben