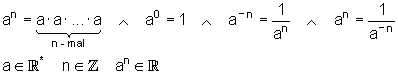In diesem Beitrag gebe ich eine Übersicht über die Rechengesetze mit Wurzeln und Potenzen. Am Schluss stelle ich ein paar Tips und Tricks bei mBerechnungen mit Wurzeln vor.
- Potenz Definition
- Potenzgesetze
- Erweiterte Potenzdefinition
- Multiplikation und Division von Potenzen mit ungleicher Basis aber gleichem Exponenten
- Potenzieren und Radizieren von Potenzen
- Zusammenfassung der Potenzgesetze
- Tips und Tricks beim Berechnungen mit Wurzeln
Potenz Definition:
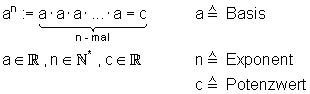
Eine Potenz ist eine Multiplikation gleicher Faktoren (Basis), bei der der Exponent die Anzahl der Faktoren angibt, zum Beispiel:
![]()
![]()
![]()
![]()
![]()
![]()
Potenzgesetze
Addition und Subtraktion von Potenzen:
Potenzen mit gleicher Basis und gleichem Exponenten kann man addieren oder subtrahieren.
Beispiele:
a) ![]()
b) ![]()
Multiplikation von Potenzen mit gleicher Basis
Potenzen mit gleicher Basis multipliziert man, indem man ihre Exponenten addiert und die Basis beibehält.
![]()
Beispiele:
a) ![]()
b) ![]()
c) ![]()
Merke

Das kannst du dir auch in diesem Video Potenzen multiplizieren ansehen.
Division von Potenzen mit gleicher Basis
Potenzen mit gleicher Basis dividiert man, indem man den Nennerexponenten vom Zählerexponenten subtrahiert und die Basis beibehält.
![]()
Der Satz kann aber laut Definition nur gelten, wenn m > n ist.
Wir untersuchen daher die Fälle m = n und m < n.
![]()
Wenn man gleiche Potenzen dividiert, erhält man im Ergebnis den Exponent 0.
Wenn man gleicher Zahlen dividiert, erhält man als Ergebnis 1.
Daher ist es sinnvoll, a0 = 1 zu definieren.
![]()
Ist der Zählerexponent kleiner als der Nennerexponent, so erhält man bei der Anwendung der Regel über die Division von Potenzen eine negative Zahl als Exponent.
Um die Allgemeingültigkeit der Regel zu erreichen, muss man die Definition des Potenzbegriffes erweitern und die Potenz mit negativen Exponenten sinnvoll interpretieren.
Setzt man eine Potenz vom Zähler in den Nenner oder umgekehrt, so ändert sich das Vorzeichen des Exponenten.
![]()
Erweiterte Potenzdefinition:
Das heißt, die Basis der Potenz kann eine reelle Zahl sein. Der Exponent kann eine ganze Zahl sein.
Eine ausführliche Erklärung der Zahlenmengen findest du im Beitrag Entwicklung der Zahlenmengen.
Eine Übersicht dazu in Standardmengen und mathematische Zeichen.
Mit Hilfe dieser Definition sind die Regeln über die Multiplikation und Division ebenfalls uneingeschränkt gültig.
Beispiele:
a)
![]() Noch deutlicher wird dies, wenn wir Zahlen einsetzen:
Noch deutlicher wird dies, wenn wir Zahlen einsetzen:
\dfrac{2^5}{2^3} =2^{5-3} = 2^2 = 4
Wenn wir den Bruch ausrechnen: \dfrac{2^5}{2^3} = \frac{32}{8} = 4 Stimmt also!
Als nächstes drehen wir den Bruch um:
\dfrac{2^3}{2^5} =2^{3-5} = 2^{-2} = \frac{1}{4} Negative Exponenten ergeben also einen Bruch!
Wieder rechnen wir den Bruch zur Probe aus:
\dfrac{2^3}{2^5} =\frac{8}{32} = \frac{1}{4} Auch hier das gleich Ergebnise!
Dies kannst du dir auch in diesem Video Potenzen dividieren und negative Exponenten.
b)
![]()
c)
![]()
d)
![]()
Multiplikation von Potenzen mit ungleicher Basis aber gleichem Exponenten
Potenzen mit ungleicher Basis aber gleichem Exponenten multipliziert man, indem man ihre Basen multipliziert und den Exponenten beibehält.
![]()
Beispiele:
a)
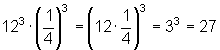
b)
![]()
Division von Potenzen mit ungleicher Basis aber gleichem Exponenten
Potenzen mit ungleicher Basis aber gleichem Exponenten dividiert man, indem man ihre Basen dividiert und den Exponenten beibehält.
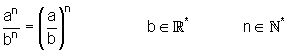
Beispiele:
a)
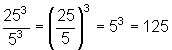
b)
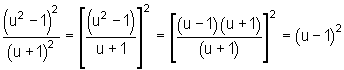
Potenzieren von Potenzen
Potenzen potenziert man, indem man die Exponenten multipliziert.
![]()
Beispiele:
a)
![]()
b)
![]()
Radizieren von Potenzen
Man zieht die Wurzel aus Potenzen, indem man den Potenzexponenten durch den Wurzelexponenten dividiert und die Basis beibehält.
![]()
Damit kann man nun alle Wurzeln als Potenzen mit rationalen Exponenten darstellen. Das vereinfacht Berechnungen mit Wurzeln, weil man sich auf die bekannten Potenzgesetze stützen kann.
Beispiele:
a) 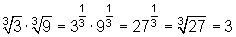
b) 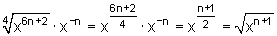
Zusammenfassung der Potenzgesetze:
Potenzen mit:
gleichen Basen multipliziert man, indem man ihre Exponenten addiert.
![]()
gleichen Basen dividiert man, indem man ihre Exponenten subtrahiert.
![]()
ungleichen Basen aber gleichen Exponenten multipliziert man, indem man die Basen multipliziert und das Produkt mit dem Exponenten versieht.
![]()
ungleichen Basen aber gleichen Exponenten dividiert man, indem man die Basen dividiert und den Quotineten mit dem Exponenten versieht.
![]()
Potenzen potenziert man, indem man ihre Exponenten multipliziert.
![]()
Jede Wurzel kann man als Potenz mit gebrochenem Exponenten geschreiben.
![]()
Der Potenzwert einer Potenz mit dem Exponenten 0 ist stets 1.
![]()
Bildet man den Kehrwert einer Potenz, so ändert sich das Vorzeichen des Exponenten.
![]()
Tipps bei Berechnungen mit Wurzeln
Faktor aus der Wurzel ziehen
Beispiele:
a)
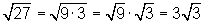
b)
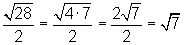
Den Nenner wurzelfrei machen
Beispiele:
a)
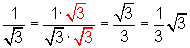
b)
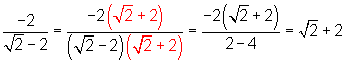
Aufgaben hierzu: Potenzen I Potenzen vereinfachen.
Hier findest du weitere Aufgaben und eine Übersicht über alle Beiträge zum Thema Potenzen und zu anderen mathematischen Grundlagen.