In diesem Beispiel erkläre ich, was Logarithmen und Logarithmengesetze sind.
- Zuerst erkläre ich anhand eines Beispiel, wofür man Logartihmen baucht.
- Danach definiere ich Logarithmen und stelle Beispiele vor.
- Dann stelle ich Logarithmen zu gebräuchlichen Basen und Sonderfälle vor.
- Anschließend stelle ich die Logarithmengesetze vor:
Logarithmus eines Produktes - eines Quotienten
- und einer Potenz.
- Danach zeige ich, wie man zwischen Logarithmensystemen umrechnet.
- Dann stelle ich Anwendungsbeispiele vor.
- Schließlich zeige ich die logarithmische Skalierungen mit Beispielen.
- Anschließend stelle ich die wichtigsten Logarithmengesetze zusammen.
- Zuletzt verlinke ich Aufgaben und weitere Beiträge.
Wofür braucht man Logarithmen?
Beim Lösen von linearen Gleichungen mit Potenzen haben wir nach dem Potenzwert und der Basis gesucht. Wie aber können wir vorgehen, wenn wir nach dem Exponenten suchen?
Wir betrachten die Gleichung 5^3 = 125
Auf der linken Seite steht eine Potenz mit der Basis 5 und dem Exponenten 3.
Auf der rechten Seite der zugehörige Potenzwert 125.
Ersetzt man Basis, Exponent oder Potenzwert durch die Variable x, dann erhält man folgende Problemstellungen.
| 5^3 = x | Der Potenzwert wird gesucht |
| x = 5^3 = 5 \cdot 5 \cdot 5 = 125 \Rightarrow L = \{125\} | Lösung durch Potenzieren |
| x^3 = 125 | Die Basis wird gesucht |
| x = \sqrt[3]{125} = 5 \, L = \{5\} | Lösung durch Wurzelziehen |
| 5^x = 125 (Exponentialgleichung) | Der Exponent wird gesucht |
| Lösung? | |
Das ist die Bestimmung des Exponenten in einer Gleichung, mit anderen Worten Logarithmieren.
Anders ausgedrückt: X ist gleich Logarithmus 125 zur Basis 5 und schreibt kurz:
x = \log_{5}(125)
Wir können die Gleichung 5^x = 125 zunächst durch Probieren lösen:
5^x = 125 \Leftrightarrow x = \log_{5}(125) \Leftrightarrow x = 3 \Rightarrow L = \{3\} \, denn \, 5^3 = 125
Logarithmus Definition:
\boxed{ x = \log_{a}(b) \Leftrightarrow a^x = b} für \, x \in \R; b \in \R_{+} \setminus \{0\}; a \in \R_{+} \setminus (0;1)
Das kannst du dir auch in diesem 
Der Logarithmus ist der Exponent (x), mit dem die Basis (a) potenziert wird, um den Potenzwert (b) zu erhalten.
Anders ausgedrückt: x ist der Logarithmus von b zur Basis a.
Beispiele:
\log_{2}(8) = 3 \, denn \, 2^3 = 8 \log_{4}(16) = 2 \, denn \, 4^2 = 16 \log_{5}(625) = 4 \, denn \, 5^4 = 625 \log_{10}(1000) = 3 \, denn \, 10^3 = 1000 \log_{a}(1) = 0 \, denn \,a^0 = 1 \log_{10}(0,1) = -1 \, denn \, 10^{-1} = \frac{1}{10} = 0,1 \log_{4}(2) = \frac{1}{2} \, denn \, 4^{\frac{1}{2}} = \sqrt{4} = 2 \log_{4}(\dfrac{1}{2}) = - \dfrac{1}{2} \, denn \, 4^{-(\frac{1}{2})} = \dfrac{1}{4^{\frac{1}{2}}} = \dfrac{1}{\sqrt{4}} = \dfrac{1}{2}
Logarithmen zu gebräuchlichen Basen
Mit dem Taschenrechner lassen sich Logarithmen zur Basis 10 und solche zur Basis e (Natürlicher Logarithmus) berechnen. Natürliche Wachstumsvorgänge werden oft durch mathematische Terme, in denen Potenzen der Zahl e enthalten sind, beschrieben. Der natürliche Logarithmus (Logarithmus Naturalis) wird in Naturwissenschaft und Technik häufig verwendet. Deshalb hat man für solche Logarithmen besondere Schreibweisen eingeführt.
\log_{10}(a) \coloneqq \lg(a) \, Logarithmus \, zur \, Basis \, 10 \, (dekadischer Logarithmus) \log_{e}(a) \coloneqq \ln(a) \, Logarithmus \, zur \, Basis \, e \, (natürlicher \, Logarithmus)
Sonderfälle
Aus der Definition des Logarithmus x = \log_{a}(b) = a^x = b folgt unmittelbar:
| \log_{a}(a) = 1 | denn \, 1 = \log_{a}(a) \Leftrightarrow a^1 = a | für den Logarithmus zur Basis a |
| \lg(10) = 1 | denn \, 1 = \lg \Leftrightarrow 10^1 = 10 | für den dekadischen Logarithmus |
| \ln(e) = 1 | denn \, 1 = \ln \Leftrightarrow e^1 = e | für den natürlichen Logarithmus |
| \log_{a}(1) = 0 | denn \, 0 = \log_{a}(1) \Leftrightarrow a^0 = 1 | für den Logarithmus zur Basis a |
| \lg(1) = 0 | denn \, 0 = \lg \Leftrightarrow 10^0 = 1 | für den dekadischen Logarithmus |
| \ln(1) = 0 | denn \, 0 = \ln \Leftrightarrow e^0 = 1 | für den natürlichen Logarithmus |
Logarithmus im Exponenten
Vielfach sind für Termumformungen folgende Beziehungen nützlich:
| x = \log_{a}(b) \Leftrightarrow a^x = b \Leftrightarrow a^{\log_{a}(b)} = b | Zahlenbeispiel: 2 = a^{log_{a}(2)} |
| x = \lg(b) \Leftrightarrow 10^x = b \Leftrightarrow 10^{\lg(b)} = b | Zahlenbeispiel: 5 = 10^{\lg(5)} |
| x = \ln(b) \Leftrightarrow e^x = b \Leftrightarrow e^{\ln(b)} = b | Zahlenbeispiel: 9 = e^{\ln(9)} |
Die Logarithmengesetze
Logarithmus eines Produktes
Der Logarithmus eines Produktes ist gleich der Summe der Logarithmen der einzelnen Faktoren.
\log_{a}(b \cdot c) = \log_{a}(b) + \log_{a}(c) Das kannst du dir auch in diesem 📽️Shorts Logarithmen multiplizieren und dividieren ansehen.
Beispiel:
\lg(500) = \lg(5 \cdot 100) = \lg(5) + \lg(100) = \lg(5) +2
Logarithmus eines Quotienten
Der Logarithmus eines Quotienten ist gleich der Differenz der Logarithmen von Dividend (Zähler) und Divisor (Nenner).
\log_{a}(\dfrac{b}{c}) = \log_{a}(b) - \log_{a}(c) Das kannst du dir ebenfalls in diesem 📽️Shorts Logarithmen multiplizieren und dividieren ansehen.
Beispiel:
\log_{7}(\dfrac{343}{7}) = \log_{7}(343) - \log_{7}(7) = \log_{7}(7)^3 - \log_{7}(7)^1 = 3 - 1 = 2
Logarithmus einer Potenz
Der Logarithmus einer Potenz ist gleich dem Logarithmus der Basis multipliziert mit dem Exponenten.
\log_{a}(b^c) = c \cdot \log_{a}(b)
Beispiel:
\log_{3}(3)^5 = 5 \cdot \log_{3}(3)^1 = 5 \cdot 1 = 5 Das kannst du dir auch in diesemShorts Logarithmus einer Potenz berechnen ansehen.
Merke:
Für Wurzeln gilt:
\log_{a}(\sqrt[c]{b}) = \log_{a}(b)^{\frac{1}{c}} = \dfrac{1}{c} \cdot \log_{a}(b)
Beispiel:
\ln(\sqrt[3]{e}) = \ln(e^{\frac{1}{3}} = \dfrac{1}{3} \ln(e) = \dfrac{1}{3}
Umrechnung zwischen Logarithmensystemen
Da mit dem Taschenrechner nur dekadische und natürliche Logarithmen berechenbar sind, ist es von Fall zu Fall notwendig Logarithmen umzurechnen.
\log_{a}(b) = \dfrac{\lg(b)}{\lg(a)} = \dfrac{\ln(b)}{\ln(a)}
Beispiel:
\log_{3}(5) = \dfrac{\lg(5)}{\lg(3)} \approx 1,4649735 Das kannst du dir auch in diesemLogarithmus mit Taschenrechner berechnen ansehen.
Beweis:
x = \log_{a}(b) \Leftrightarrow a^x = b
und
y = \log_{c}(b) \Leftrightarrow c^y = b \newline \Leftrightarrow a^x = c^y \vert \log_{c}() \Leftrightarrow \log_{c}(a^x) = \log_{c}(c^y) \Leftrightarrow x \cdot \log_{c}(a) = y \cdot \underbrace{\log_{c}(c)}_{1} \Leftrightarrow x \cdot \log_{c}(a) = y
Für x und y die Logarithmen einsetzen und nach
\log_{a}(b)
umstellen:
\log_{a}(b) \cdot \log_{c}(a) = \log_{c}(b) \, \big \vert : \log_{c}(a) \log_{a}(b) = \dfrac{\log_{c}(b)}{\log_{c}(a)} = \dfrac{\lg(b)}{\lg(a)} = \dfrac{\ln(b)}{\ln(a)}
Anwendungsbeispiele
Der Bruchterm soll zur Basis 10 logarithmiert werden.
\dfrac{a^2 \cdot b \cdot \sqrt[3]{c}}{d \cdot \sqrt{e^3}}\newline \lg \left(\dfrac{a^2 \cdot b \cdot \sqrt[3]{c}}{d \cdot \sqrt{e^3}} \right) = \lg \left(\dfrac{a^2 \cdot b \cdot c^{\frac{1}{3}}}{d \cdot e^{\frac{3}{2}}} \right) = 2 \cdot \lg(a) + \lg(b) + \dfrac{1}{3} \cdot \lg(c) - \lg(d) - \dfrac{3}{2} \cdot \lg(e)
Die Logarithmenterme sollen zu einem Logarithmenterm zusammengefasst werden.
\ln(x) - \frac{1}{2} \ln(y) + \frac{4}{5} \ln(z) \ln(x) - \frac{1}{2} \cdot \ln(y) + \frac{4}{5} \cdot \ln(z) = \ln\left( \dfrac{x \cdot z^{\frac{4}{5}}}{y^{\frac{1}{2}}} \right) = \ln\left( \dfrac{x \cdot \sqrt[5]{z^4}}{\sqrt{y}} \right)
Umformungen mit Logarithmus im Exponenten.
2^x = e^{\ln(2^x)} = e^{\ln(2)x} 4^x = 10^{\lg(4^x)} = 10^{\lg(4)x} e^{\ln(10)x} = e^{\ln(10^x)} = 10^x 10^{\lg(e)x} = 10^{\lg(e^x)} = e^x
Logarithmische Skalierung
Beispiel:
Die Graphen der Funktion \color{red}{f(x) = 10^x} und \color{blue}{g(x) = 10 \cdot e^x} sollen in einem Koordinatensystem dargestellt werden.
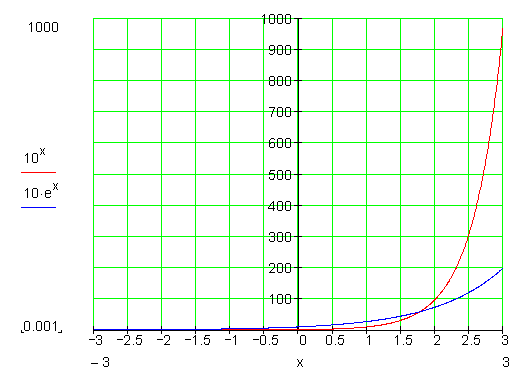
Ein Nachteil dieser Darstellung ist, dass Funktionswerte für kleine x-Werte nicht mehr abgelesen werden können.
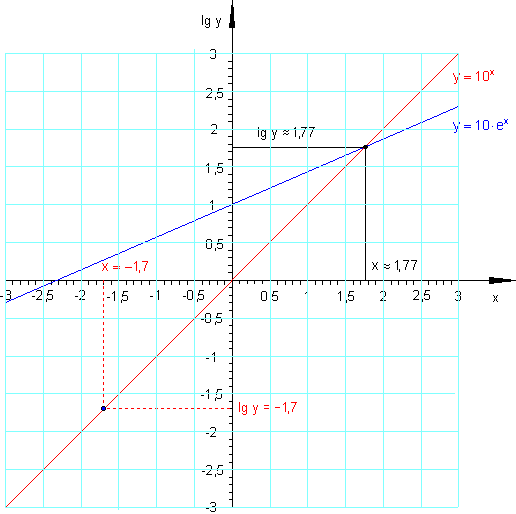
Bei einer logarithmischen Skalierung der y-Achse werden die Graphen zu Geraden. Auf der y-Achse werden die Logarithmen der Funktionswerte abgetragen.
1. Funktion in der logarithmischen Darstellung
y = 10^x \Leftrightarrow \lg(y) = \lg(10^x) = x \cdot \lg(10) = x \color{red}{\Rightarrow \lg(y) = x}
Gerade durch den Ursprung mit der Steigung 1
Zu dieser Funktion könnt ihr euch das 📽️Video Logarithmische Darstellung ansehen.
2. Funktion in der logarithmischen Darstellung
y = 10 \cdot e^x \Leftrightarrow \lg(y) = lg(10 \cdot e^x) = \lg(10) + x \cdot \lg(e) = 1 + x \cdot \lg(e) \Rightarrow \color{blue}{\lg(y) = \lg(e) \cdot x + 1}
Gerade mit der Steigung lg(e)
Die tatsächlichen Werte müssen berechnet werden.
Der Wert -1,7 auf der y-Achse bedeutet
\lg(y) = -1,7 \Rightarrow y = 10^{-1,7} \approx 0,02
Der Schnittpunkt des Graphen der Funktionen
f(x) = 10^x mit dem der Funktion g(x) = 10 \cdot e^x
wird bei logarithmischer Skalierung der y-Achse auf den Schnitt zweier Geraden zurückgeführt.
f(x) = g(x) \Leftrightarrow 10^x = 10 \cdot e^x (Exponentialgleichung)
Lösung durch Logarithmieren:
\Rightarrow \lg(10^x) = \lg(10 \cdot e^x) \Leftrightarrow x \cdot \lg(10) = \lg(10) + x \cdot \lg(e) \Leftrightarrow x \cdot 1 = 1 + x \cdot \lg(e) \Leftrightarrow x - x \cdot \lg(e) = 1 \Leftrightarrow x (1 - \lg(e)) = 1 \Leftrightarrow x = \frac{1}{1 - \lg(e)} \approx 1,77 \lg(y) = \lg(10^x) = x \cdot \lg(10) = x \approx 1,77 \lg(y) = \lg(10 \cdot e^x) = \lg(10) + x \cdot \lg(e) = 1 + x \cdot 0,434 \approx 1,77 f(x) \approx 10^{1,77} \approx 58,88 \Rightarrow S(1,77 | 58,88) Schnittpunkt zweier Graphen
Kontrolle:
g(x) \approx 10 \cdot e^1,77 \approx 58,70 (Abweichungen durch Rundung)
Beispiel Logarithmische Skalierungen:
Nach Gabe eines medizinischen Präparates stirbt ein Bakterienstamm nach der Funktion
N(t) = N_0 \cdot e^{-\gamma \cdot t}
ab.
Dabei bedeuten:
N(t) Anzahl der Bakterien nach der Zeit t N_0 Anzahl der Bakterien zum Zeitpunkt t=0 \gamma Abklingkonstante
Die Zeit, nach der die Hälfte der Bakterien abgestorben ist, wird Halbwertszeit \tau genannt.
Graphisch lässt sich dieser Vorgang wie folgt darstellen:
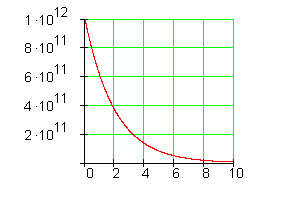
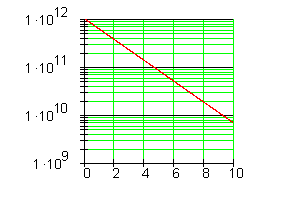
Stelle einen Zusammenhang zwischen der Abklingkonstanten \gamma und der Halbwertszeit \tau dar.
Halbwertszeit:
Aus N(\tau) = \frac{1}{2} \cdot N_0 und N(\tau) = N_0 \cdot e^{- \gamma \cdot \tau} folgt \frac{1}{2} \cdot N_0 = N_0 \cdot e^{- \gamma \cdot \tau} \Leftrightarrow \frac{1}{2} = e^{- \gamma \cdot \tau} e^{- \gamma \cdot \tau} = \frac{1}{2} \, \, \, \, \vert logarithmieren \Leftrightarrow \ln(e^{- \gamma \cdot \tau}) = \ln(\frac{1}{2}) \, \, \, \, \vert umformen \Leftrightarrow - \gamma \cdot \tau \underbrace{\ln(e)}_{1} = \ln(1) - \ln(2) \, \, \, \, \vert : \tau \Leftrightarrow \gamma \cdot \tau = \ln(2) - \ln(1) \, \, \, \, \vert : \tau \Leftrightarrow \gamma = \frac{\ln(2) - \underbrace{\ln(1)}_{0}}{\tau} \Leftrightarrow \gamma = \frac{\ln(2)}{\tau}
Damit kann man auch schreiben:
\underline{\underline{N(t) = N_0 \cdot e^{- \frac{\ln(2)}{\tau} \cdot t}}}
Bemerkung:
Die Halbwertszeit ist die Zeit, in der sich ein exponentiell mit der Zeit abnehmender Wert halbiert hat.
Die wichtigsten Logarithmengesetze:
1. Logarithmus zur Basis a
| x = \log_a(b) \Leftrightarrow a^x = b | \log_a(b \cdot c) = \log_a(b) + \log_a(c) |
| \log_a (\frac{b}{c} = \log_a(b) - \log_a(c) | \log_a(b^{c}) = c \cdot \log_a(b) |
| \log_a(a) = 1 \log_a(1) = 0 |
b = a^{\log_a(b)} b^{x = a^{x \cdot \log_a(b)} } |
2. Logarithmus zur Basis 10 (Zehner- oder dekadischer Logarithmus) [LOG]-Taste
| x = \lg(b) \Leftrightarrow 10^{x} = b | \lg(b \cdot c) = \lg(b) + \lg(c) |
| \lg(\frac{b}{c}) = \lg(b) - \lg(c) | \lg(b^{c}) = c \cdot \lg(b) |
| \lg(10) = 1 \lg(1) = 0 |
b = 10^{\lg(b)} b^{x} = 10^{x \cdot \lg(b)} |
3. Logarithmus zur Basis e (Natürlicher Logarithmus oder Logarithmus Naturalis)
| x = \ln(b) \Leftrightarrow e^{x} = b | \ln(b \cdot c) = \ln(b) + \ln(c) |
| \ln(\frac{b}{c} = \ln(b) - \ln(c) | \ln(b^{c}) = c \cdot \ln(b) |
| \ln(e) = 1 \ln(1) = 0 |
b = e^{\ln(b)} b^{x} = e^{x \cdot \ln(b)} |
4. Umrechnung von einem Logarithmensystem in ein anderes.
| \log_a(b) = \frac{\lg(b)}{\lg(a)} = \frac{\ln(b)}{\ln(a)} | \log_3(5) = \frac{\lg(5)}{\lg(3)} = \frac{\ln(5)}{\ln(3)} \approx 1,4649735 |
