|
|
Aufgaben |
|
|
|
| <<< voriges Aufgabenblatt | Lösungen teilen | nächstes Aufgabenblatt >>> |
| Nr. | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 |
| 1. | Berechnen Sie die Kurvenpunkte mit waagerechter Tangente. Sind diese Kurvenpunkte Extrempunkte? Begründen Sie Ihre Entscheidung. | ||||||
| a) |
|
b) |
|
c) |
|
Lösung | |
| 2. | Berechnen Sie die lokalen Extrempunkte des Graphen der Funktion f(x). Zeichnen Sie den Graphen in ein geeignetes Koordinatensystem. |
|
Lösung |
| 3. | Bestimmen Sie a so, dass die Funktion f(x)in x = 2 eine Extremstelle hat. Um welche Art von Extremstelle handelt es sich dabei? |
|
Lösung |
| 4. | Gegeben ist eine Funktion f(x). Bestimmen Sie a so, dass der Extrempunkt des Graphen von f(x) auf der x- Achse liegt. Ist der Extrempunkt ein Hoch - oder ein Tiefpunkt? |
|
Lösung |
| 5. | Die Funktion f(x) soll keine Extremstellen besitzen. Welche Bedingungen müssen für diesen Fall die Koeffizienten erfüllen und wie viele Nullstellen hat dann f(x)? Begründen Sie Ihre Antwort. |
|
Lösung |
| 6. |
 Die Verbindungsgerade von Hoch und Tiefpunkt begrenzt mit den Koordinatenachsen ein Dreieck. Berechnen Sie den Inhalt der Dreiecksfläche in Abhängigkeit von a. Fertigen Sie zuvor eine Skizze an. |
Lösung |
| 7. | Untersuchen Sie auf Extrempunkte: | ||
| a) |
|
||
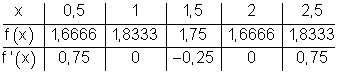
| b) |
|
Lösung | |
| 8. |
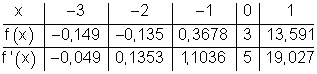
Berechnen Sie Extrem- und Wendepunkte der Graphen folgender Funktionen: Berechnen Sie außerdem von Aufgabe 1, 4, 5, 6, und 7 die Achsenschnittpunkte und zeichnen Sie den Graphen. |
||||
| a) |
|
b) |
|
||
| c) |
|
d) |
|
||
| e) |
|
f) |
|
||
| g) |
|
Lösung | |||