Hier findest du die Aufgaben der Lösungen zu Funktionen V.
1. Bestimme den maximalen Definitionsbereich Dmax
Alle vier Aufgaben kannst du dir auch in dem 📽️ Video Funktionen Definitionsmenge ansehen.
a)
![]()
b)
![]()
Dazu kannst du die Mengenschreibweise nachlesen.
c)
![]()
d)
![]()
2. Bestimme den Wertebereich
a)
![]()
b)
![]()
c)
![]()
d)
![]()
3. Gegeben ist die Funktion f(x).
a)
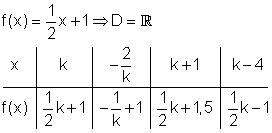
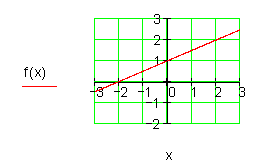
b)
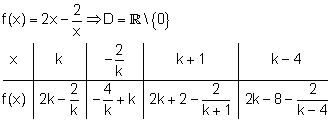
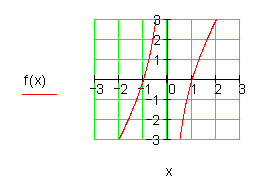
c)
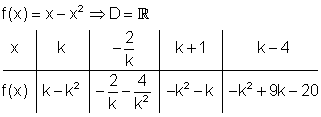
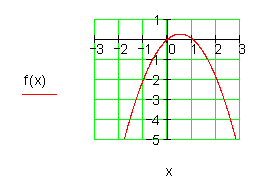
d)
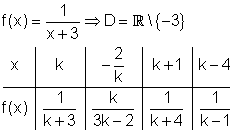
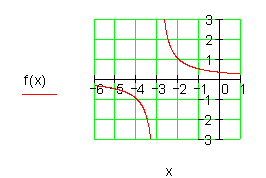
e)
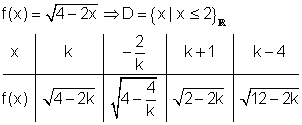
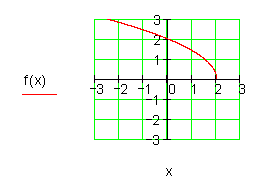
f)
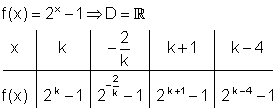
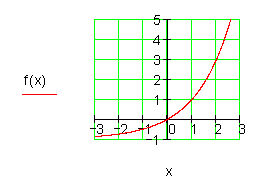
4. Gegeben ist die Funktion
a)
![]()
b)
![]()
c)
![]()
d)
![]()
5. Die Funktion f(x) ist definiert für D = IR.
a)
![]()
b)
![]()
Hier findest du die Aufgaben.
Und hier Aufgaben zu Fnktionen VII.
Die Theorie findest du hier: Relationen und Funktionen.
Und Funktionen in der Mathematik.
Hier findest du eine Übersicht über weitere Beiträge zu linearen Funktionen, darin auch Links zu weiteren Aufgaben.
