Hier findest du die Aufgaben zu Funktionen VII.
1. Gegeben sind folgende Funktionen.
Erstellen Sie eine geeignete Wertetabelle! Zeichne den dazugehörigen Graphen!
a)
![]()
b)
![]()
2. Welcher Graph gehört zu einer Funktion
f: \rightarrow f(x) Begründe es!
a)
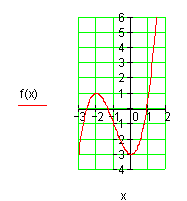
b)
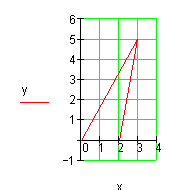
c)
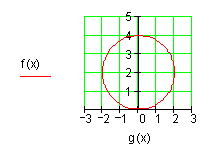
3. Formuliere mit Hilfe der mathematischen Kurzschreibweise.
a) An der Stelle 3 hat die Funktion f(x) den Funktionswert 12.
b) Durch die Funktion f(x) wird dem x- Wert die Zahl -4 zugeordnet.
c) Der Punkt P ( 2 | 5 ) liegt auf dem Schaubild von f(x).
d) Für welches Argument hat f(x) den Funktionswert 4.
e)
![]()
f)Die Funktion f(x) nimmt an der Stelle -17 den Funktionswert 9 an.
g)Die Funktionen f und g nehmen an der Stelle x = 3 denselben Funktionswert an.
h)An welcher Stelle x ist der Funktionswert von f kleiner als der Funktionswert g?
i)
![]()
j)Die Koordinaten eines Kurvenpunktes Kf stimmen überein.
4. Nenne ein alltägliches Beispiel
für eine Zuordnung, die eine bzw. keine Funktion ist!
5. Die nebenstehende Kurve
ist der Graph der Funktion f(x). Lese aus dem Graphen ab:
a) Den Funktionswert an der Stelle 5
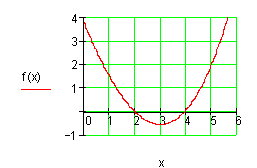
b) Eine Stelle x mit f ( x ) = 0
c) Auf welchem Bereich gilt f ( x ) > 0?
6. Welche der Wertetabellen können zu einer Funktion gehören?
a)
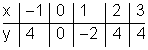
b)
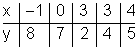
Hier findest du die Lösungen
und hier Aufgaben zu Funktionen II
Die Aufgaben Relationen I, III und VI und weitere Unterrichtsmaterialien sind in den Materialien enthalten, die Sie in unserem Shop erwerben können.
Die Theorie findest du hier: Relationen und Funktionen
und Funktionen in der Mathematik.
Hier eine Übersicht über alle Beiträge zur Linearen Funktionen.
