Hier findest du die Lösungen der Aufgaben mit Exponentialgleichungen und e-Funktionen.
1. a) Löse die Gleichung!
Ausführliche Lösung:
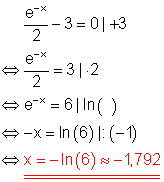
Wir formen die Gleichung zunächst so um, dass auf beiden Seiten möglichst einfache Ausdrücke stehen. Dann logarithmieren wir unter Anwendung der bekannten Logarithmengesetze.
Hier kannst du nochmal alles zu Logarithmen nachlesen.
Und hier die Playlist aller Videos dazu: 📽️ Videos zu Logarithmen.
1. b)
Löse die Gleichung!
Ausführliche Lösung:
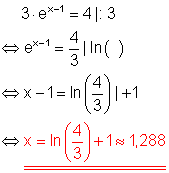
Wir formen die Gleichung zunächst so um, dass auf beiden Seiten möglichst einfache Ausdrücke stehen. Dann logarithmieren wir unter Anwendung der bekannten Logarithmengesetze.
1. c)
Löse die Gleichung!
Ausführliche Lösung:
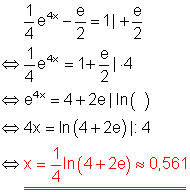
1. d)
Löse die Gleichung!
Ausführliche Lösung:
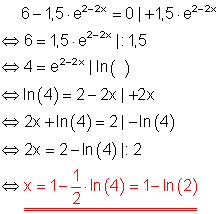
1. e)
Löse die Gleichung!
Ausführliche Lösung:
2,5^{kx} = 12 \, \, \, \, k \not=0 2,5^{kx} = 12 \, \, \, \, \vert : 2,5 \Leftrightarrow e^{kx} = 4,8 \, \, \, \, \vert \ln() \Leftrightarrow kx = \ln(4,8) \, \, \, \, \vert :k \Leftrightarrow \color{red}{\underline{\underline{x = \frac{1}{k} \ln(4,8)}}}
1. f)
Löse die Gleichung!
Ausführliche Lösung:
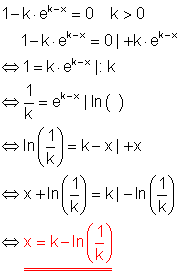
1. g)
Löse die Gleichung!
Ausführliche Lösung:
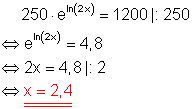
1. h)
Löse die Gleichung!
Ausführliche Lösung:
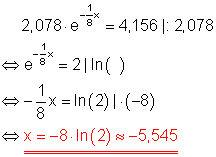
1. i)
Löse die Gleichung!
Ausführliche Lösung:
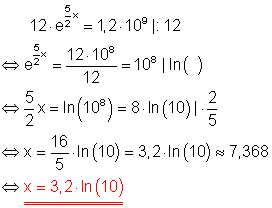
2. a) Löse die Gleichung!
Ausführliche Lösung:
2 \cdot e^{3x} - 6 \cdot e^{x} = 0 \, \, \, \, \vert +6 \cdot e^{x} \Leftrightarrow 2 \cdot e^{3x} = 6 \cdot e^{x} \, \, \, \, \vert :2 \Leftrightarrow e^{3x} = 3 \cdot e^{x} \, \, \, \, \vert \ln() \Leftrightarrow 3x = \ln(3) + x \, \, \, \, \vert -x \Leftrightarrow 2x = \ln(3) \, \, \, \, \vert :2 \Leftrightarrow \color{red}{\underline{\underline{x = \frac{1}{2} \cdot \ln(3)}}}
2. b)
Löse die Gleichung!
Ausführliche Lösung:
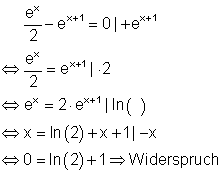
Tritt bei den Lösungsschritten ein Widerspruch auf, so hat die Gleichung keine Lösung.
2. c)
Löse die Gleichung!
Ausführliche Lösung:
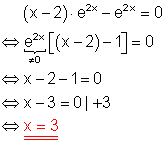
Der Satz vom Nullprodukt wurde angewendet.
2. d)
Lösee die Gleichung!
Ausführliche Lösung:
![]()
Nach dem Satz vom Nullprodukt muss x2 = 0 sein und damit auch x. Denn ein Produkt ist genau dann Null, wenn mindestens ein Faktor Null ist. Da die e-Funktion für keinen x-Wert Null werden kann, muss also x2 Null sein.
2. e)
Löse die Gleichung!
Ausführliche Lösung:
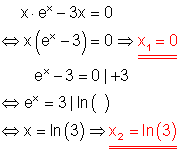
Der Satz vom Nullprodukt wurde angewendet.
2. f)
Löse die Gleichung!
Ausführliche Lösung:
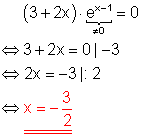
Der Satz vom Nullprodukt wurde angewendet.
3. a) Löse die Gleichung!
Ausführliche Lösung:
e^{2x} - \frac{17}{2}e^{x} + 16 = 0 Substitution: e^{x} = u \Leftrightarrow e^{2x} = u^{2} \Leftrightarrow u^{2} - \frac{17}{2}u + 16 = 0 quadratische Gleichung \Rightarrow p = - \frac{17}{4} ; \, q=16 D = (\frac{p}{2})^{2}-q = (- \frac{17}{2})^{2} - 16 = \frac{289}{4} - \frac{64}{4} = \frac{225}{4} \Rightarrow \sqrt{D} = \sqrt{\frac{225}{4}} = \frac{15}{2} u_{1/2}= - \frac{p}{2} \pm \sqrt{D} u_1 = \frac{17}{2} + \frac{15}{2} = \frac{32}{2} = 16 u_2 = \frac{17}{2} - \frac{15}{2} = \frac{2}{2} = 1 u_1 = 16 \Leftrightarrow e^{x} = 16 \, \, \, \, \vert \ln() \Leftrightarrow \color{red}{\underline{\underline{x_1=\ln(16)}}} u_2 = 1 \Leftrightarrow e^{x}= 1 \, \, \, \, \vert \ln() \Leftrightarrow x_2 = \ln(1) \Leftrightarrow \color{red}{\underline{\underline{x_2 = 0}}}
3. b)
Löse die Gleichung!
Ausführliche Lösung:
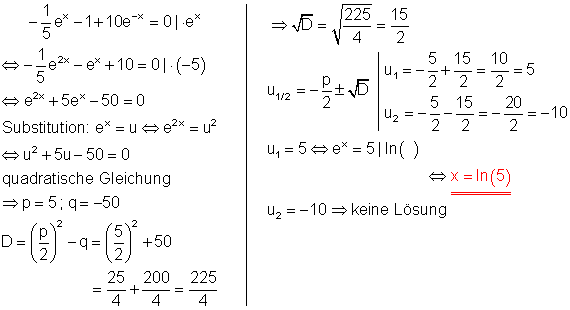
Die Multiplikation der Gleichung mit ex vereinfacht den Term. Für u2 gibt es keine Lösung, da u2 negativ und für negative Zahlen kein Logarithmus definiert ist.
3. c)
Löse die Gleichung!
Ausführliche Lösung:
e^{-2x} - 10e^{-x} + 9 = 0 \, \, \, \, \vert \cdot e^{2x} \\ \Leftrightarrow 1 - 10e^{x} + 9e^{2x} = 0 \\ \Leftrightarrow 9e^{2x} - 10e^{x} + 1 = 0 \, \, \, \, \vert :9 \\ \Leftrightarrow e^{2x} - \frac{10}{9}e^{x} + \frac{1}{9} = 0
Substitution: e^{x} = u \\ \Leftrightarrow e^{2x} = u^{2} \\ \Leftrightarrow u^{2} - \frac{10}{9}u + \frac{1}{9} =0
Quadratische Gleichung: \Rightarrow p_0 -\frac{10}{9} ; \, q=\frac{1}{9} \\ D = (\frac{p}{2})^{2} - q = (-\frac{5}{9})^{2} - \frac{1}{9} = \frac{25}{81} - \frac{9}{81} = \frac{16}{81} \\ \Rightarrow \sqrt{D} = \sqrt{\frac{16}{81}} = \frac{4}{9} \\ u_{1/2} = - \frac{p}{2} \pm \sqrt{D} \\ u_1 = \frac{5}{9} + \frac{4}{9} = \frac{9}{9} = 1 \\ u_2 = \frac{5}{9} - \frac{4}{9} = \frac{1}{9} \\ u_1 = 1 \Leftrightarrow e^{x} = 1 \, \, \, \, \vert \ln() \\ \Leftrightarrow x = \ln(1) \Leftrightarrow \color{red}{\underline{\underline{x_1 = 0}}} u_2 = \frac{1}{9} \Leftrightarrow e^{x} = \frac{1}{9} \, \, \, \, \vert \ln() \\ \Leftrightarrow x = \ln(\frac{1}{9}) \Leftrightarrow \color{red}{\underline{\underline{x_2 = - \ln(9)}}}
3. d)
Löse die Gleichung!
Ausführliche Lösung:
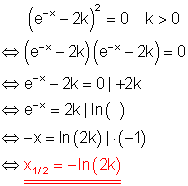
Lösungsweg:
Das Quadrat des Klammerausdrucks wird als Produkt dargestellt. Der Satz vom Nullprodukt wird angewendet. Da beide Klammern identisch sind, ist das Ergebnis als doppelte Nullstelle zu werten.
3. e)
Löse die Gleichung!
Ausführliche Lösung:
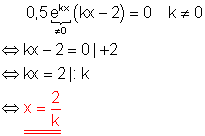
Lösungsweg:
Zur Lösung der Aufgabe wenden wir den Satz vom Nullprodukt an. Nur der Klammerausdruck kann Null werden.
3. f)
Löse die Gleichung!
Ausführliche Lösung:
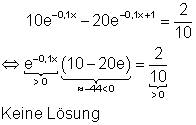
Die Gleichung hat keine Lösung. Der Wert der e-Funktion vor der Klammer ist für alle x größer Null. Der Klammerausdruck ist negativ, so dass auch das Produkt auf der linken Seite negativ ist. Das steht im Widerspruch zu dem Wert der rechten Seite, der positiv ist.
4. a) Löse die Gleichung!
Ausführliche Lösung:
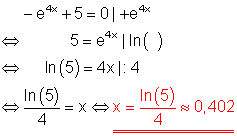
4. b)
Löse die Gleichung!
Ausführliche Lösung:
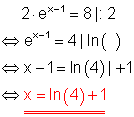
4. c)
Löse die Gleichung!
Ausführliche Lösung:
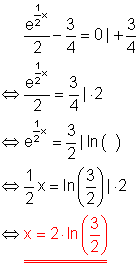
4. d)
Löse die Gleichung!
Ausführliche Lösung:
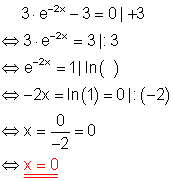
Der Logarithmus zu einer beliebigen Basis von 1 ist immer Null.
4. e)
Löse die Gleichung!
Ausführliche Lösung:
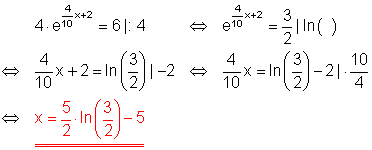
4. f)
Löse die Gleichung!
Ausführliche Lösung:
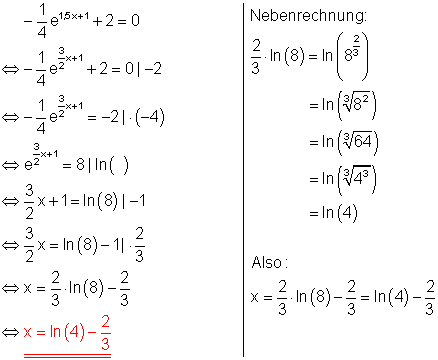
5. a) Löse die Gleichung!
Ausführliche Lösung:
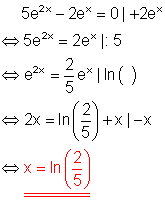
5. b)
Löse die Gleichung!
Ausführliche Lösung:
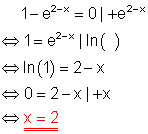
Der Logarithmus zu einer beliebigen Basis von 1 ist immer Null.
5. c)
Löse die Gleichung!
Ausführliche Lösung:
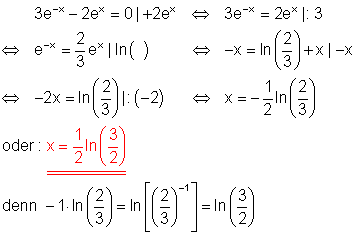
5. d)
Löse die Gleichung!
Ausführliche Lösung:
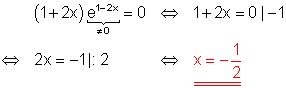
Der Satz vom Nullprodukt wird angewendet.
5. e)
Löse die Gleichung!
Ausführliche Lösung:
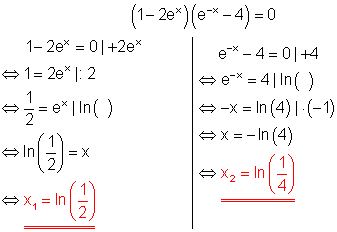
Der Satz vom Nullprodukt wird angewendet. Jede der beiden Klammern wird Null gesetzt. Es gibt zwei unterschiedliche Lösungen.
5. f)
Löse die Gleichung!
Ausführliche Lösung:
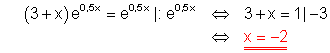
6. a) Löse die Gleichung!
Ausführliche Lösung:
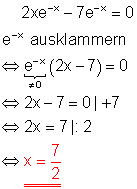
Der Satz vom Nullprodukt wird angewendet. Da die e-Funktion für keinen x-Wert Null werden kann, muss also der Klammerausdruck Null sein.
6. b)
Löse die Gleichung!
Ausführliche Lösung:
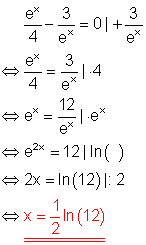
6. c)
Löse die Gleichung!
Ausführliche Lösung:
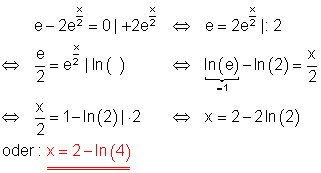
6. d)
Löse die Gleichung!
Ausführliche Lösung:
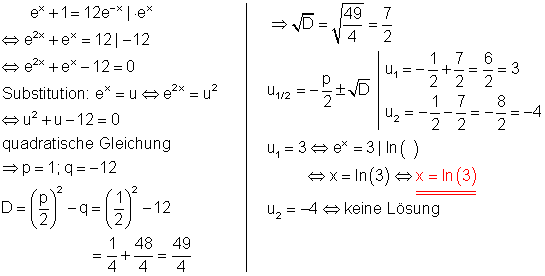
Für u2 gibt es keine Lösung, weil für negative Zahlen kein Logarithmus definiert ist.
6. e)
Löse die Gleichung!
Ausführliche Lösung:
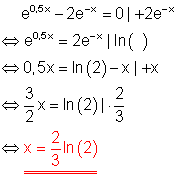
6. f)
Löse die Gleichung!
Ausführliche Lösung:
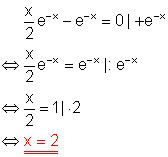
6. g)
Löse die Gleichung!
Ausführliche Lösung:
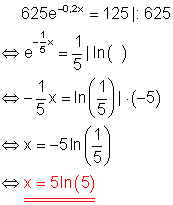
6. h)
Löse die Gleichung!
Ausführliche Lösung:
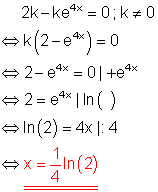
Wir wenden den Satz vom Nullprodukt an. Da entsprechend der Vorgabe k ungleich Null ist, kann nur der Klammerausdruck Null werden.
6. i)
Löse die Gleichung!
Ausführliche Lösung:
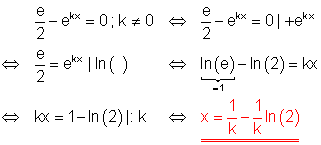
7. a) Löse die Gleichung!
Ausführliche Lösung:
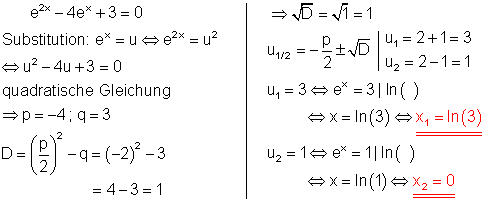
7. b)
Löse die Gleichung!
Ausführliche Lösung: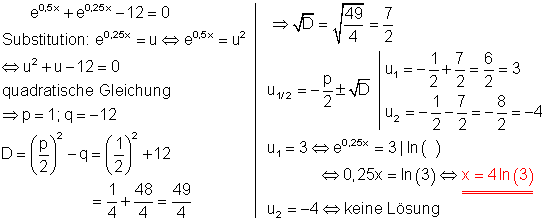
7. c)
Löse die Gleichung!
Ausführliche Lösung:
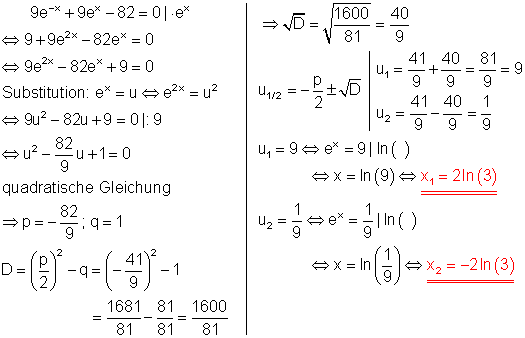
7. d)
Löse die Gleichung!
Ausführliche Lösung: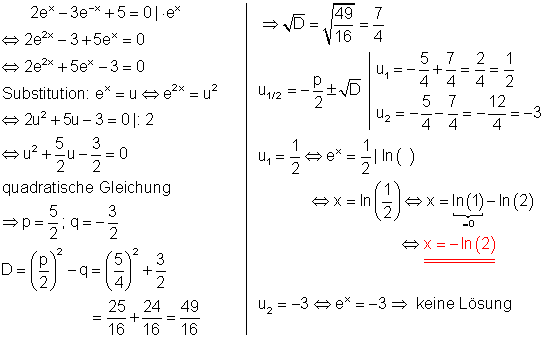
Für u2 gibt es keine Lösung, weil für negative Zahlen kein Logarithmus definiert ist.
7. e)
Löse die Gleichung!
Ausführliche Lösung: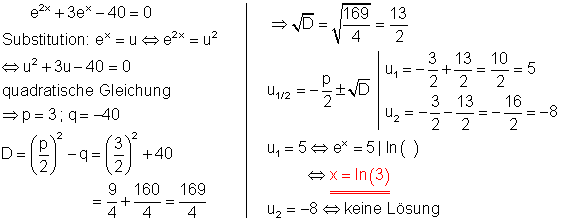
Für u2 gibt es keine Lösung, weil für negative Zahlen kein Logarithmus definiert ist.
7. f)
Löse die Gleichung!
Ausführliche Lösung: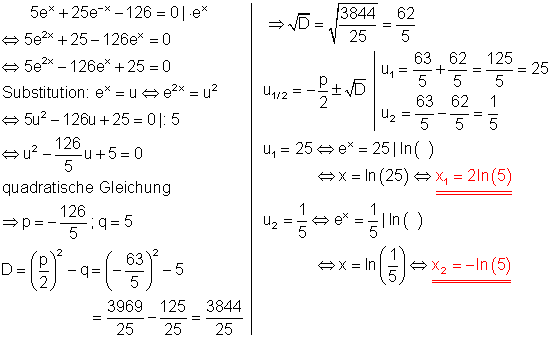
Hier findest du die Aufgaben hierzu.
Und hier die Theorie: Exponentialgleichungen.
Eine große Hilfe bieten die Regeln zum Lösen von Exponentialgleichungen.
Hier kannst du nochmal alles zu Logarithmen nachlesen.
Und hier die Playlist aller Videos dazu: 📽️ Videos zu Logarithmen.
Hier eine Übersicht über weitere Beiträge zu Gleichungen, darin auch Links zu weiteren Aufgaben.
